不同的二叉搜索树

题目描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的二叉搜索树有多少种? 返回满足题意的二叉搜索树的种数。

示例：

输入：n = 3
输出：5

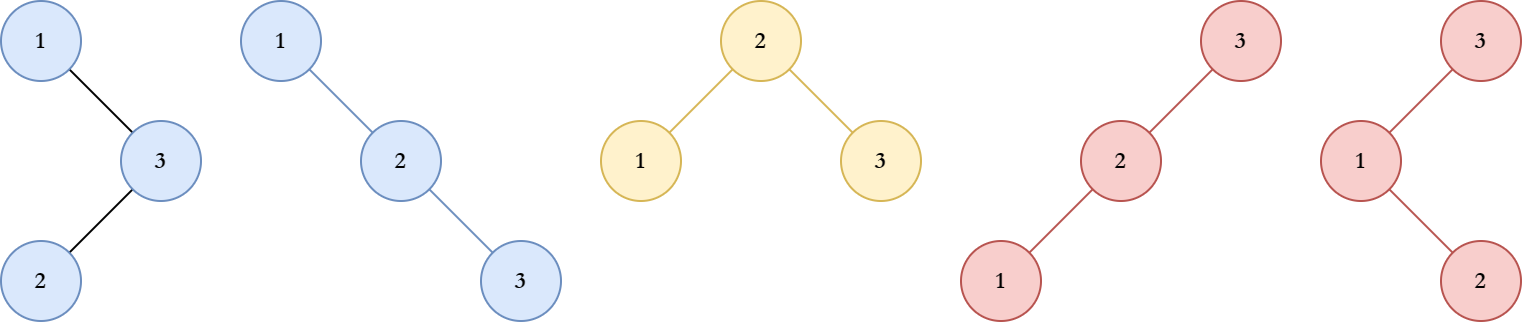
解题思路

对于 n 个数，我们分别以每个数作为根节点，因为根节点是不一样的，所以产生的树是不会重复的。我们记 n 能够形成 $G(n)$ 个二叉搜索树，以数字 i 为根节点能产生 $F(i)$ 个二叉搜索树，则可以得到

$$
G(n) = \sum_{i = 1}^{n} F(i)
$$

对于以 i 为节点，那么 $[1, i -1]$ 总共 $i - 1$ 个数形成它的左子树，而 $[i + 1, n]$ 总共 $n - i$ 个数形成它的右子树，所以我们可以得到。由 $G(n)$ 的定义可知，左子树总共有 $G(i - 1)$ 种可能，而右子树有 $G(n-i)$ 种可能，所以得到以 i 为根节点，总共有

$$
F(i) = G(i - 1) \times G(n - i)
$$

从而得到 $G(n)$ 的递归表达式

$$
G(n) = \sum_{i = 1}^{n} G(i - 1) \times G(n - i)
$$

public int numTrees(int n) {
    int[] dp = new int[n + 1];
    dp[0] = 1;
    dp[1] = 1;
    if (n == 0 || n == 1) {
        return dp[n];
    }
    for (int i = 2; i <= n; i++) {
        for (int j = 1; j <= i; j++) {
            dp[i] += (dp[j - 1] * dp[i - j]);
        }
    }
    return dp[n];
}