最长回文字符串

题目描述

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例 2：

输入: "cbbd"
输出: "bb"

暴力法

扫描一遍字符串，判断 $[i, j]$ 范围内的字符串是不是回文字符串，并且在这个过程中记录最长的字符串

class Solution {
    public String longestPalindrome(String s) {

        if (s == null || s.length() < 2) {
            return s;
        }

        char[] str = s.toCharArray();
        int start = 0;
        int maxLength = 1;

        for (int i = 0; i < str.length - 1; i++) {
            for (int j = i + 1; j < str.length; j++) {
                // 如果 [i,j] 范围的字符串长度小于目前已知的最长回文字符串的长度，则无需判断
                if ((j - i + 1) > maxLength) {
                    // 如果是回文字符串，更新最长回文字符串的长度，以及该回文字符串的起始位置
                    if (isPalindrome(str, i, j)) {
                        maxLength = j - i + 1;
                        start = i;
                    }
                }
            }
        }

        return s.substring(start, start + maxLength);
    }

    // 判断 [start, end] 范围内的字符串是否为回文字符串
    private boolean isPalindrome(char[] str, int start, int end) {
        while (start <= end) {
            // 判断两端的字符串是否相同,不相同则不可能是回文字符串
            if (str[start] != str[end]) {
                return false;
            }
            start++;
            end--;
        }

        return true;
    }
}

动态规划

我们开辟一个数组 $dp$，$dp[i][j]$ 表示 $[i, j]$ 范围内的字符串是否为回文字符串，那我们可以知道

$$
dp[i][j] =
\begin{cases}
false, \quad &when \quad str[i] \neq str[j] \\
dp[i+1][j-1], \quad &when \quad str[i] = str[j]
\end{cases}
$$

当 $str[i] \neq str[j]$ 的时候，那么不可能是回文字符串，如果 $str[i] = str[j]$ 的时候，如果 $dp[i+1][j-1]$ 是回文字符串，那么 $dp[i][j]$ 就是回文字符串。

但是如果 $i + 1 > j - 1$ 的话，这时 $dp[i + 1][j - 1]$ 没有意义，其实这种情况就是 $[i,j]$ 内只有两个字符，如果 $str[i] = str[j]$ 的话，那么它就是一个回文字符串，所以这时可以直接得到 $dp[i][j] = true$。

class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 2) {
            return s;
        }

        int length = s.length();
        boolean dp[][] = new boolean[length][length];
        for (int i = 0; i < length; i++) {
            for (int j = 0; j < length; j++) {
                dp[i][j] = false;
            }
        }

        // [i,i] 表示单个字符，肯定是回文字符串
        for (int i = 0; i < length; i++) {
            dp[i][i] = true;
        }

        int maxLength = 1;
        int begin  = 0;
        // 因为 [i, j] 要用到 [i + 1, j - 1]，所以让 i 动
        // 如果让 j 动，那么 [i + 1, j -1] 的范围没都判断过，会导致错误的结果
        for (int j = 1; j < length; j++) {
            for (int i = 0; i < j; i++) {
                // 如果字符两端不相等，不是回文字符串
                if (s.charAt(i) != s.charAt(j)) {
                    dp[i][j] = false;
                } else {
                    // 如果只有两个元素，可以直接判断为回文字符串
                    if (i + 1 > j - 1) {
                        dp[i][j] = true;
                    } else {
                        // 与 dp[i + 1][j - 1] 相同
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }

                // 更新最长长度以及起始位置
                if (dp[i][j] && (j - i + 1) > maxLength) {
                    maxLength = j - i + 1;
                    begin = i;
                }
            }
            
        }

        return s.substring(begin, begin + maxLength);
    }
}

中间扩散法

上面的情况都是检查某个范围内的字符串是否是回文字符串，而中心扩散法，则是以某点为中心进行向外扩散，在扩散的同时检查是否是回文字符串，过程如下

1. 检查该点左右两边的字符串是否相等，如果相等则继续扩散，如果不相等则停止扩散
2. 停止扩散后记录该回文字符串的长度，如果大于当前记录的最大回文字符串的长度，则进行更新，为了获得该回文字符串，还需要记录该回文字符串的起始位置

需要注意的是，既可以从某个字符开始扩散，也可以从字符间的空隙进行扩散

从某个点进行扩散的代码如下：

private int centerSpread(String s, int left, int right) {
    int length = 0;
    while(left >=0 && right < s.length()) {
        if (!(s.charAt(left) == s.charAt(right))) {
            break;
        }
        length++;
        left--;
        right++;
    }

    return length;
}

如果从某个字符进行扩散，那么 left 和 right 都是该字符的下标，如果从某个字符空隙进行扩散，则 left 和 right 分别为该空隙左右两边字符的下标。扩散的示意图如下

完整代码如下

class Solution {
    public String longestPalindrome(String s) {
        int begin = 0;
        int maxLength = 1;

        for (int i = 1; i < s.length(); i++) {
            // 从字符空隙进行扩散
            int length1 = centerSpread(s, i - 1, i);
            // 从字符进行扩散
            int length2 = centerSpread(s, i, i);

            // 获得二者进行扩散的回文字符串的最大长度
            int length = (2 * length1) >= (2 * length2 - 1) ? 2 * length1 : (2 * length2 - 1);
            // 如果比 maxLength 大，则进行更新
            if (length > maxLength) {
                maxLength = length;
                begin = i - length/2;
            }
        }

        return s.substring(begin, begin + maxLength);
    }

    private int centerSpread(String s, int left, int right) {
        int length = 0;
        while(left >=0 && right < s.length()) {
            if (!(s.charAt(left) == s.charAt(right))) {
                break;
            }
            length++;
            left--;
            right++;
        }

        return length;
    }
}

Manacher算法

Manacher 算法是对中间扩散法的改进，首先我们在字符间填充 # 以此充当字符空隙，得到一个新的字符串，然后用一个数组记录新字符串每个字符能够扩散多远

b	#	a	#	b	#	a	#	d

我们复用中心扩散法的代码

class Solution {
    public String longestPalindrome(String s) {
        int begin = 0;
        int maxLength = 1;
        // babad => b#a#b#a#d
        String str = String.join( "#", s.split(""));

        for (int i = 1; i < str.length(); i++) {
            int length = centerSpread(str, i, i);
            length = 2 * length - 1;
            if (length >= maxLength) {
                // #a# b#b 二者长度相同，但是应选择后面的
                if (length > maxLength || str.charAt(i + length/2) != '#') {
                    maxLength = length;
                    begin = i - length/2;
                }
            }
        }

        // b#a#b => bab
        return String.join( "", str.substring(begin, begin + maxLength).split("#"));
    }

    private int centerSpread(String s, int left, int right) {
        int length = 0;
        while (left >= 0 && right < s.length()) {
            if (!(s.charAt(left) == s.charAt(right))) {
                break;
            }
            length++;
            left--;
            right++;
        }

        return length;
    }
}

这个时候我们还没有使用上面提到的数组，接下来我们需要利用数组记录一些信息，从而加快中间扩散法的速度。

首先我们要知道如何加快中间扩散法的速度，这就需要利用回文字符串的特点，那就是回文字符串是左右对称的，当我们对回文字符串内的某个字符进行中间扩散时，我们可以先找到对称位置的字符，看看它能够扩散的多远

如果它扩散的距离小于所处回文字符串的范围，那么根据对称的特点，我们不需要对该字符进行中间扩散，它能够扩散的距离就是对称位置所能扩散的距离

但是对称位置能够扩散的距离刚好在所处回文字符串的边界，或者大于所处的回文字符串，那么此时扩散的距离就不等于对称位置能够扩散的距离，而是需要进行扩散才能确定

但是我们不需要从该字符串开始进行扩散，因为我们可以确定在回文字符串的范围内，它是对称的，所以我们只需要从回文字符串的外部进行扩散即可

扩散完毕后记录能够扩散后的距离，并决定是否更新 begin，maxLength。

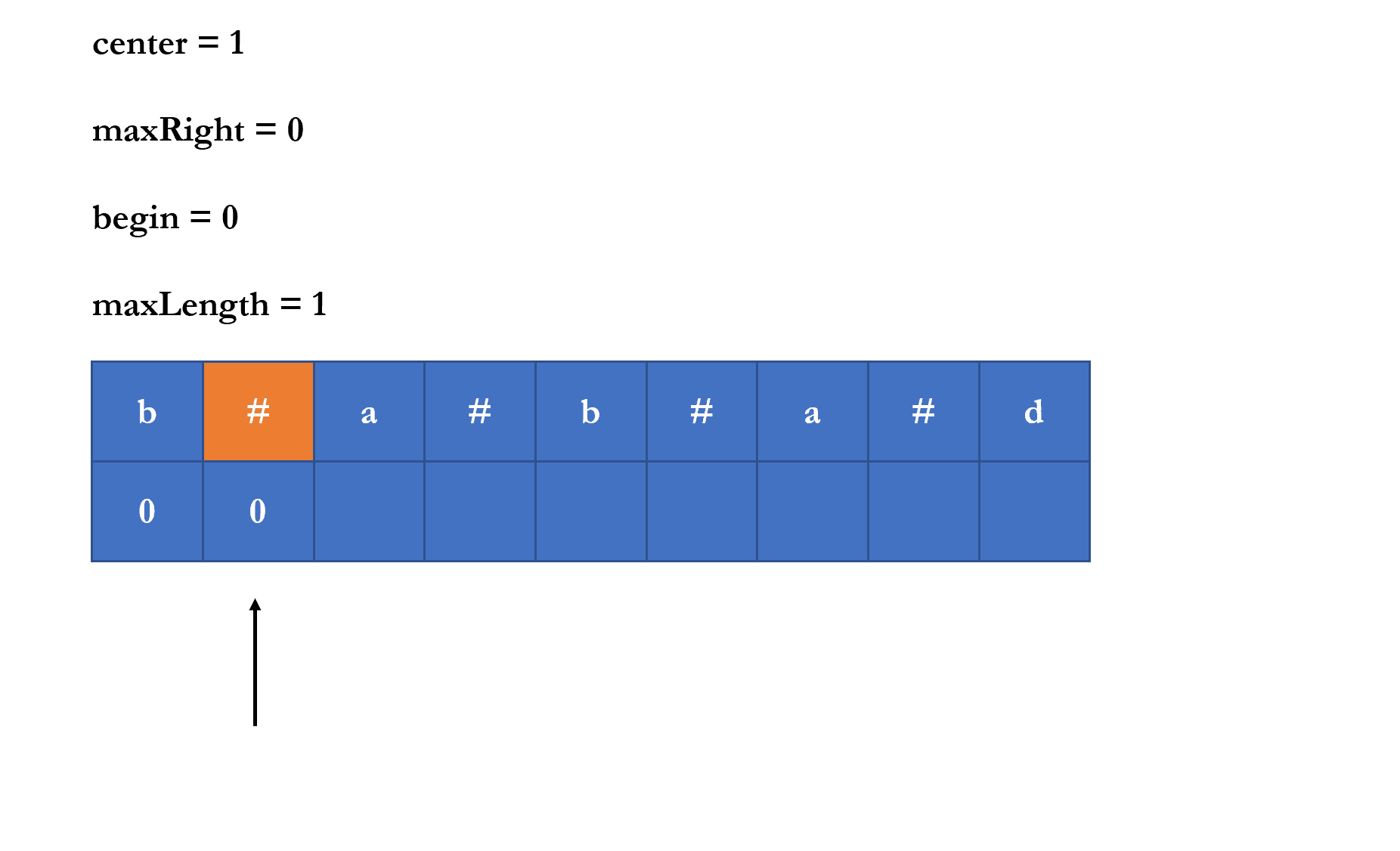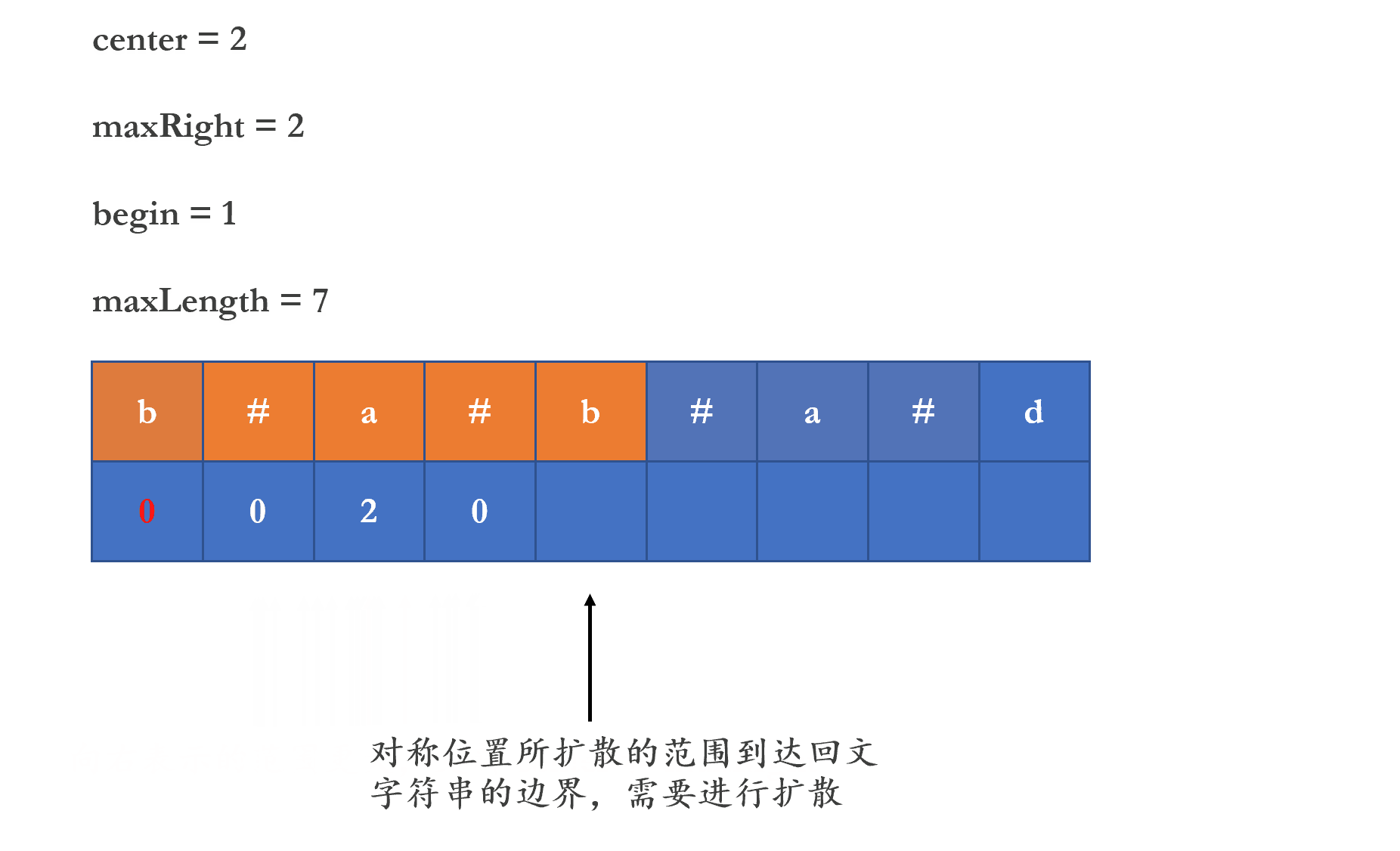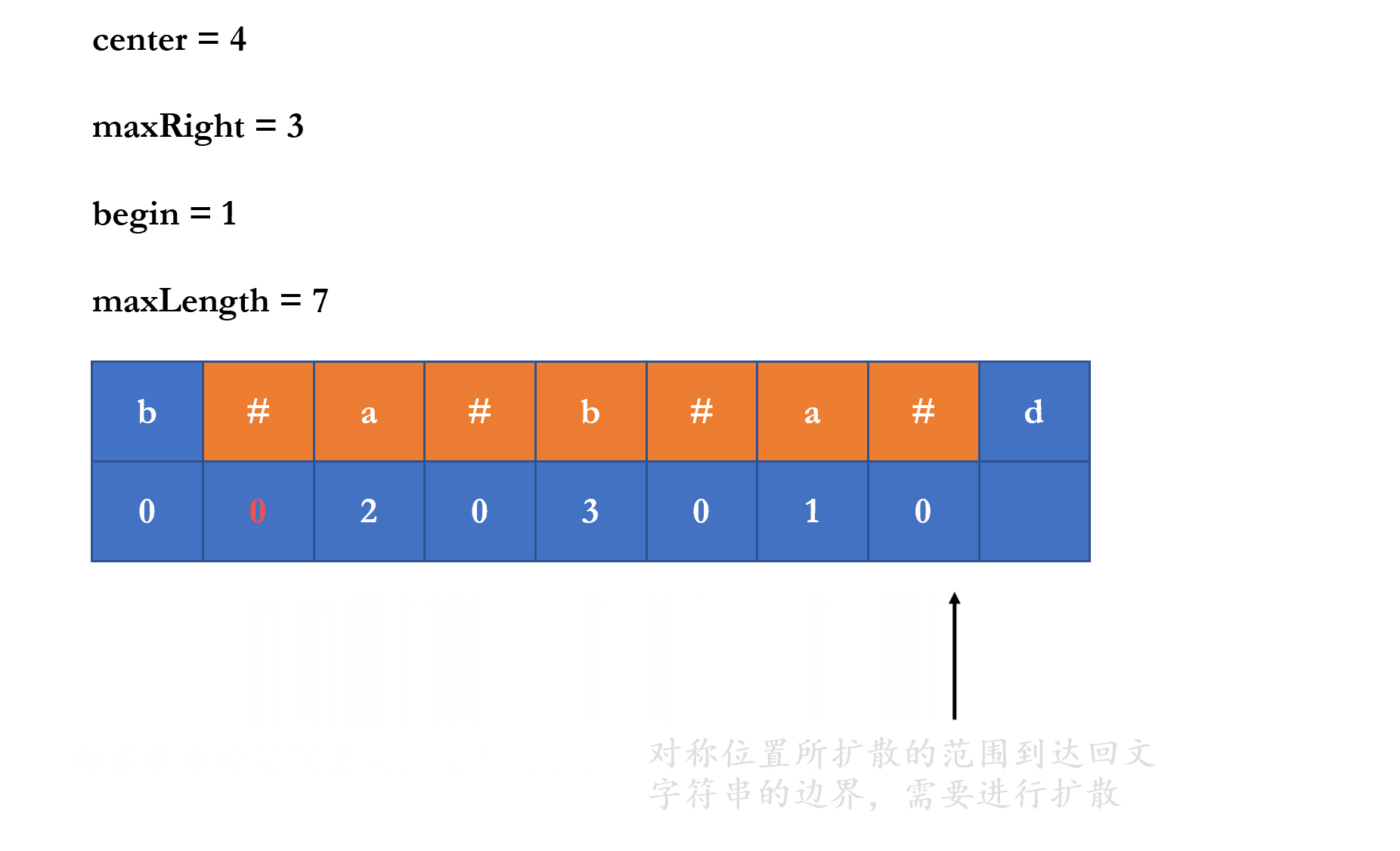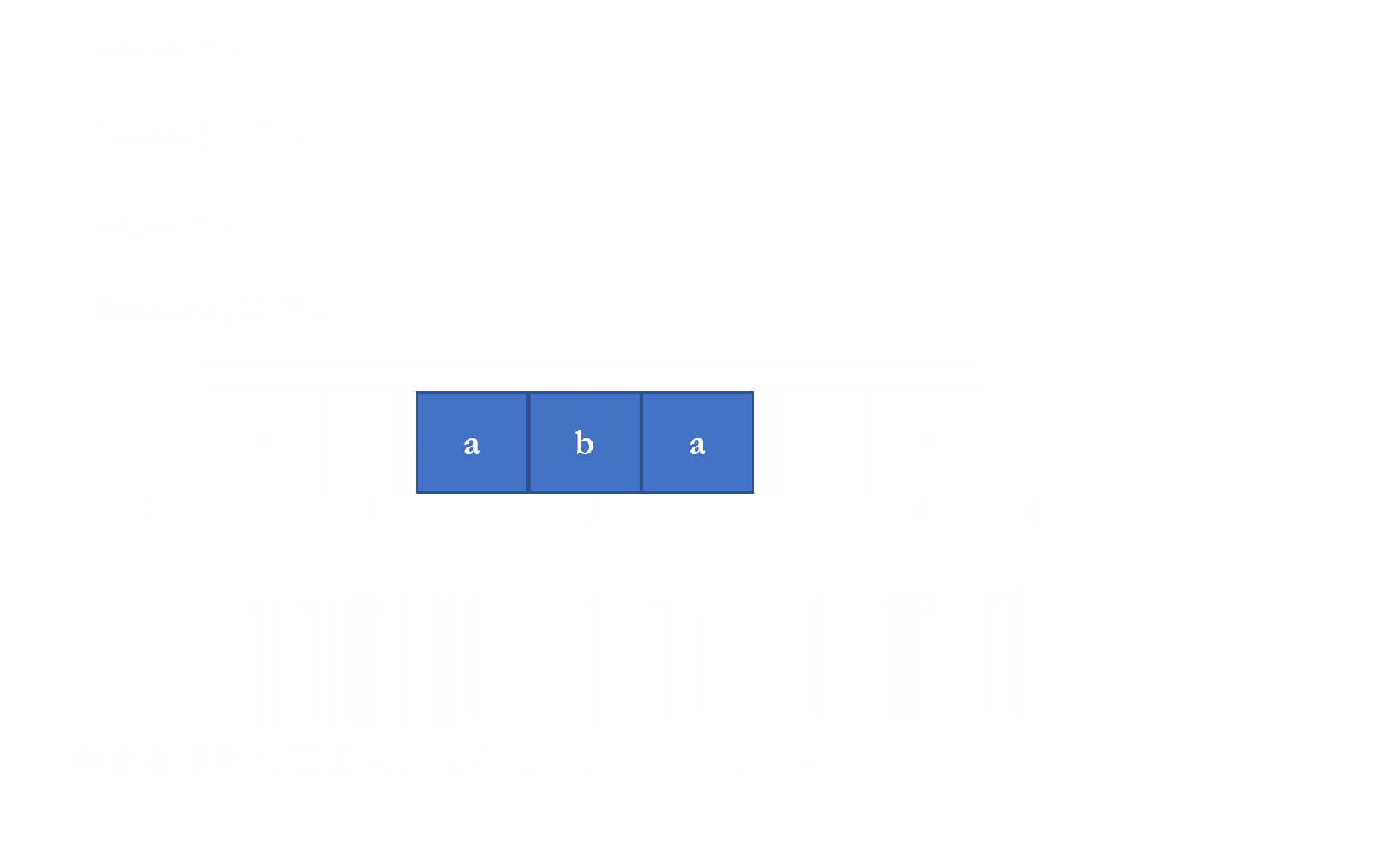
现在还有一个问题，如何知道某个字符处于一个回文字符串中，我们通过记录两个变量 center 和 maxRight 来表示一个回文字符串，center 表示回文字符串的中心，maxRight 表示中心离回文字符串右边界的距离

我们认为如果字符的下标小于 $center + maxRight$，那么它就在一个回文字符串中。

那什么时候更新这两个变量呢? 那就是在某个字符扩散之后，他向右边能够扩散的范围大于当前的 $center + maxRight$，那么就更新 center 和 maxRight。

代码如下：

class Solution {
    public String longestPalindrome(String s) {
	    // 将字符串转化为 a#b#c#b 的形式
        // String newStr = String.join( "#", s.split(""));
        StringBuilder stringBuilder = new StringBuilder();
        for (int i = 0; i < s.length(); i++) {
            if (i != s.length() - 1) {
                stringBuilder.append(s.charAt(i) + "#");
            } else {
                stringBuilder.append(s.charAt(i));
            }
        }
        String newStr = stringBuilder.toString();

         // records[i] 表示扩散距离
        int[] records = new int[newStr.length()];

        records[0] = 0;
		// 回文字符串的起始位置和长度
        int begin = 0;
        int maxLength = 1;
		// 表示回文字符串
        int center = 0;
        int maxRight = 0;

        for (int i = 1; i < newStr.length(); i++) {
		    // 如果 str[i] 在某个回文字符串中
            if (i <= center + maxRight) {
			   // 对称位置的扩散距离
                int mirrorLength = records[2 * center - i];
			   // 超过或等于 center + maxRight 表示的边界，进行中间扩散，并进行必要的更新
                if (i + mirrorLength >= center + maxRight) {
                    // 扩散
                    int length = center + maxRight - i;
                    while (i + length + 1 < newStr.length() && (i -length - 1) >= 0) {
                        if (newStr.charAt(i + length + 1) != newStr.charAt(i - length - 1)) {
                            break;
                        }
                        length++;
                    }
                    records[i] = length;
                    
                    // 更新
                    if (2 * length + 1 >= maxLength) {
                        if (2 * length + 1 > maxLength || newStr.charAt(center) != '#') {
                            begin = i - length;
                            maxLength = 2 * length + 1;
                        }
                    }

                    if (i + length > center + maxRight) {
                        center = i;
                        maxRight = length;
                    }

                } else {
				   // 小于 center + maxRight 形成的边界，直接使用对称位置的值
                    records[i] = mirrorLength;
                }
            } else {
			   // 不在回文字符串中，进行中心扩散，并进行必要的更新
                int length = 0;
                while (i + length + 1 < newStr.length() && (i - length - 1) >= 0) {
                    if (newStr.charAt(i + length + 1) != newStr.charAt(i - length - 1)) {
                        break;
                    }
                    length++;
                }

                if (2 * length + 1 > maxLength) {
                    begin = i - length;
                    maxLength = 2 * length + 1;
                }

                center = i;
                maxRight = length;
                records[i] = length;
            }
        }

	    // 将 a#b#b#a 形式的字符串转化为 abba
        // return String.join( "", newStr.substring(begin, begin + maxLength).split("#"));
        String ss = newStr.substring(begin, begin + maxLength);
        StringBuilder stringBuilder1 = new StringBuilder();
        for (int i = 0; i < ss.length(); i++) {
            if (ss.charAt(i) != '#') {
                stringBuilder1.append(ss.charAt(i));
            }
        }

        return stringBuilder1.toString();
    }
}