图的广度优先遍历

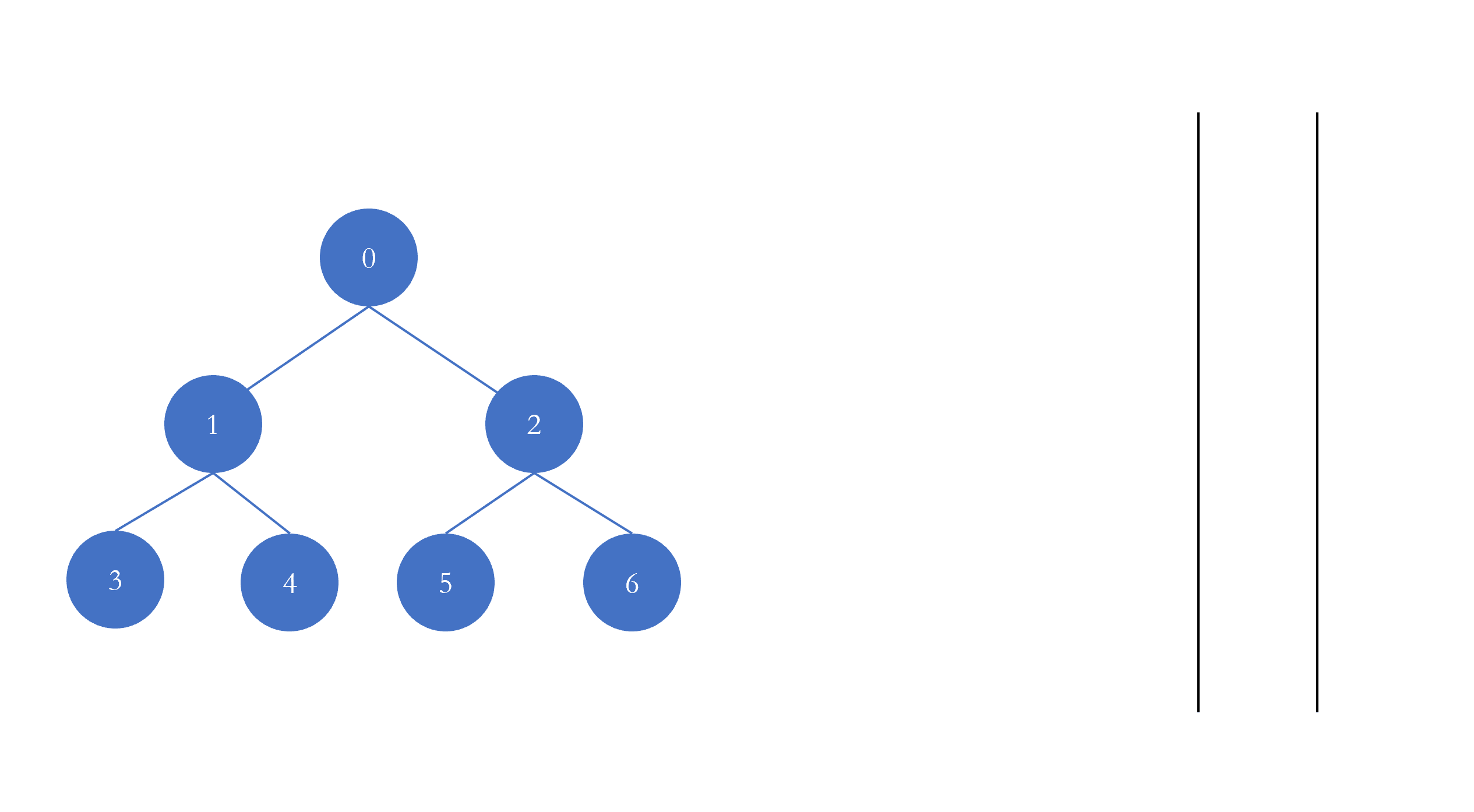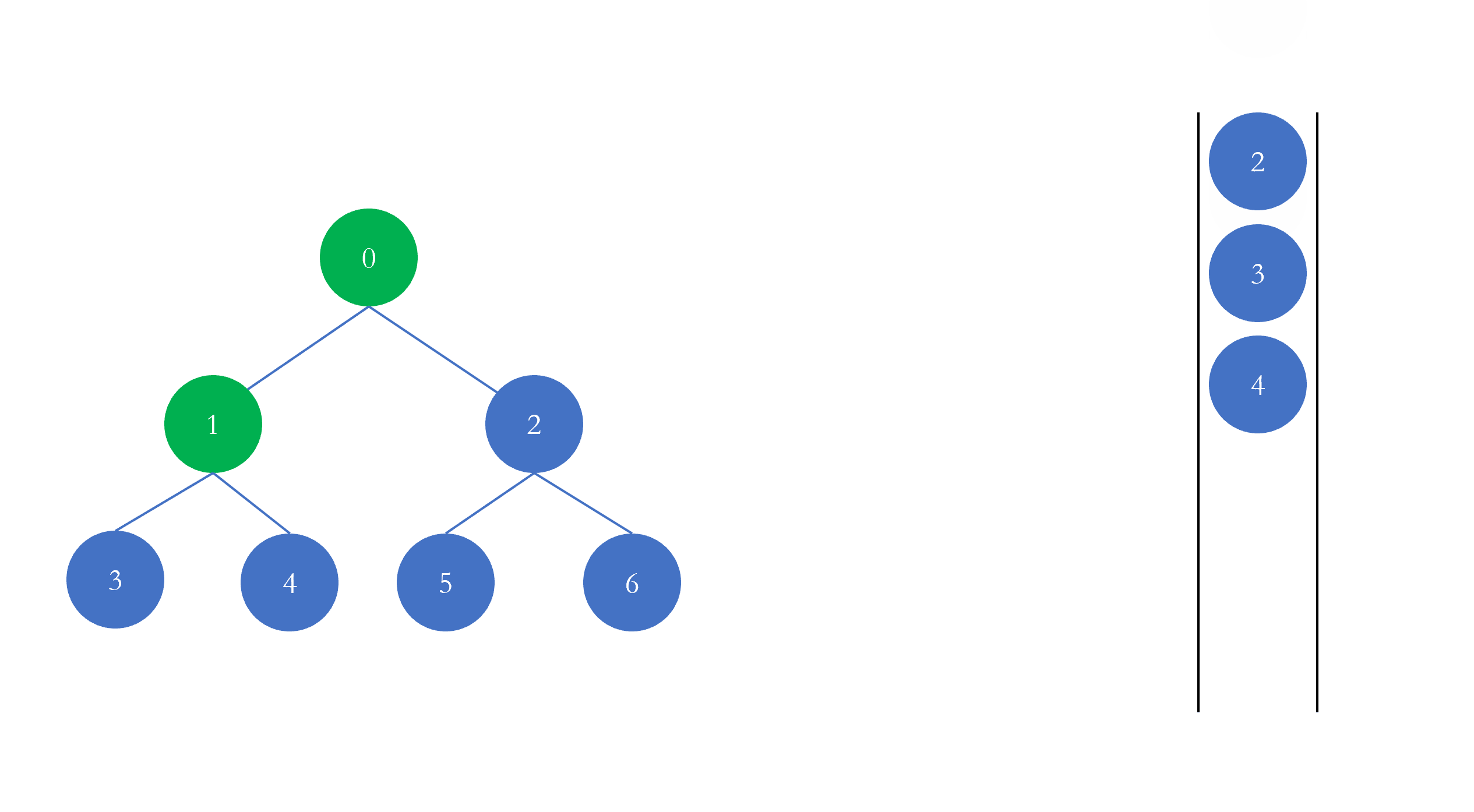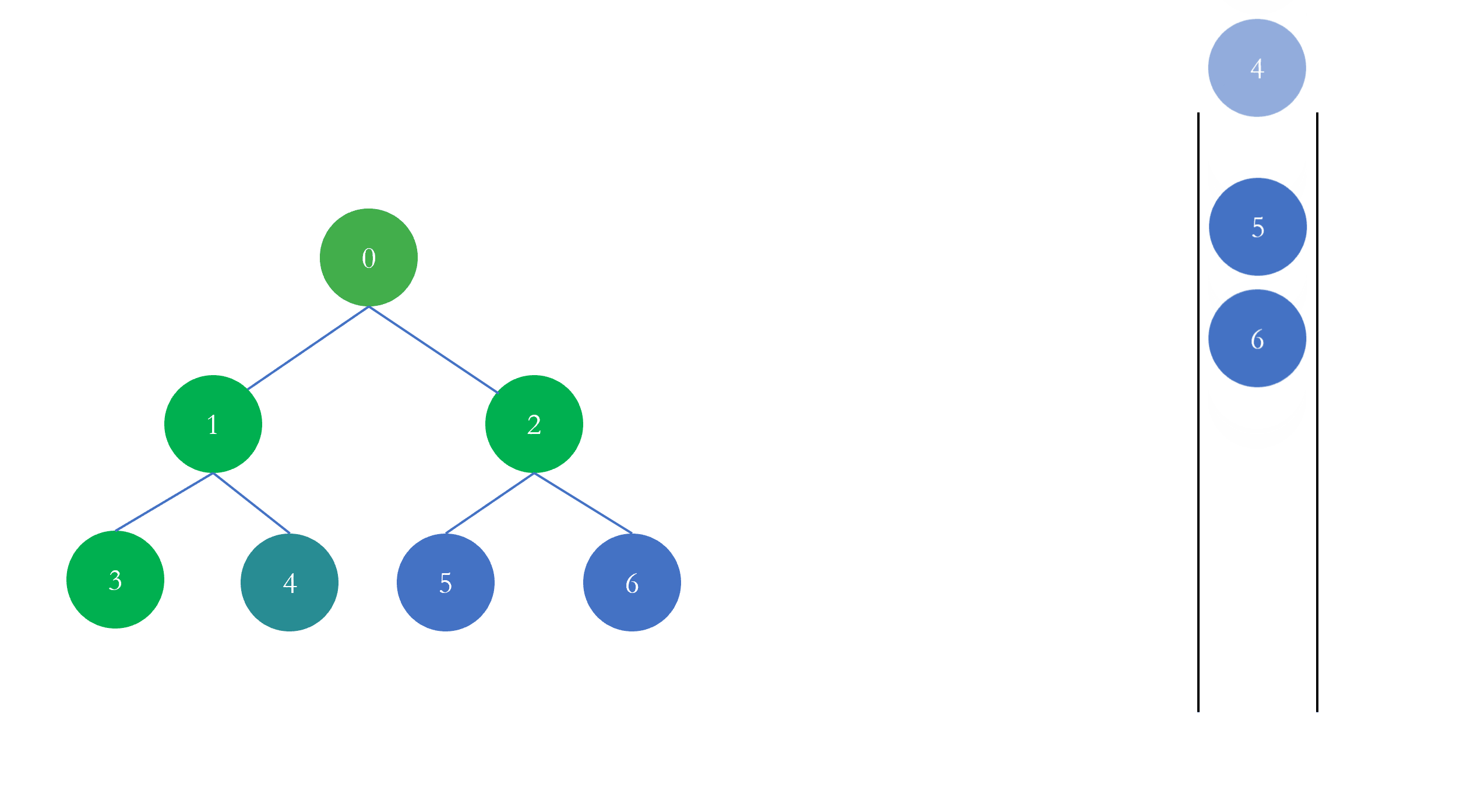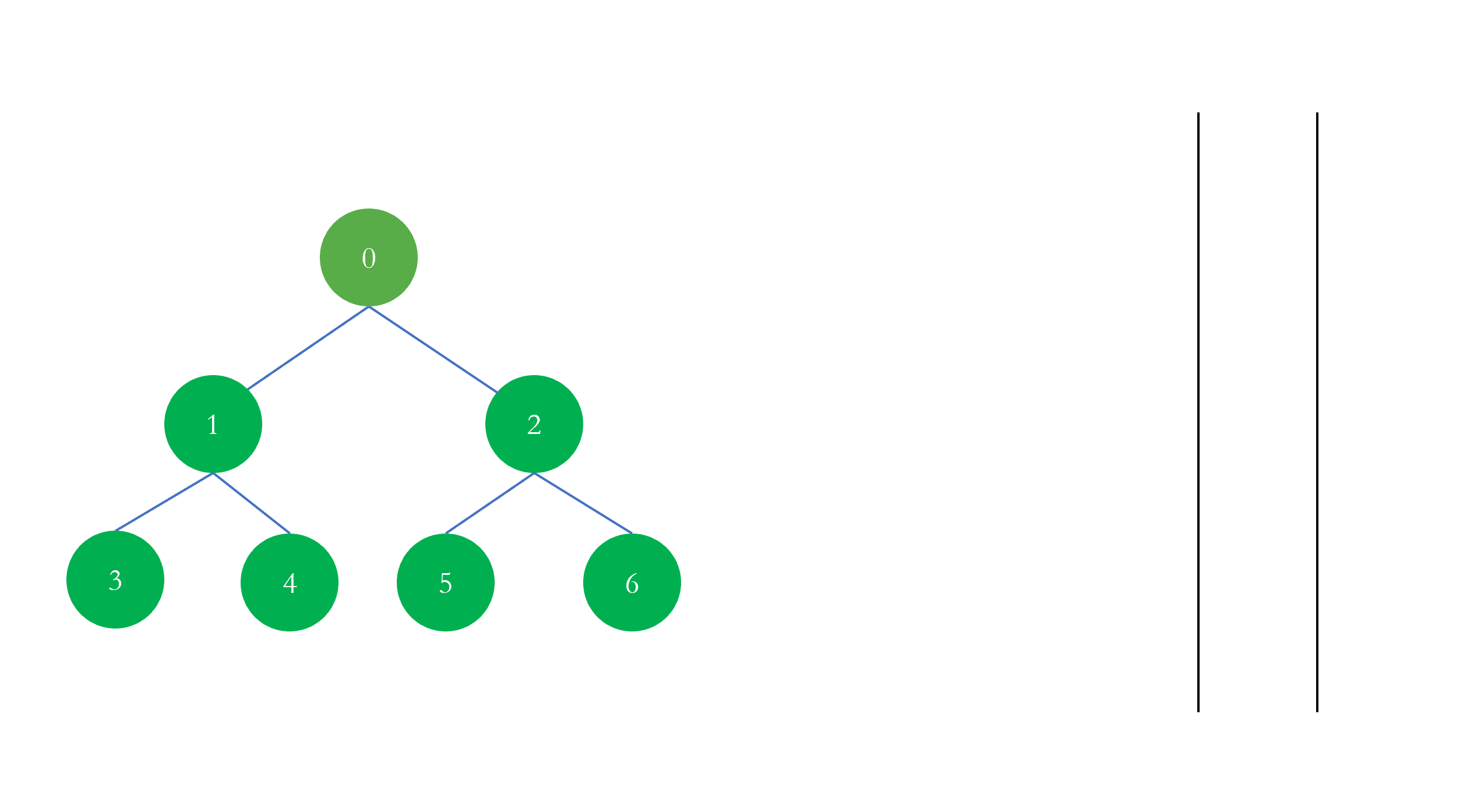
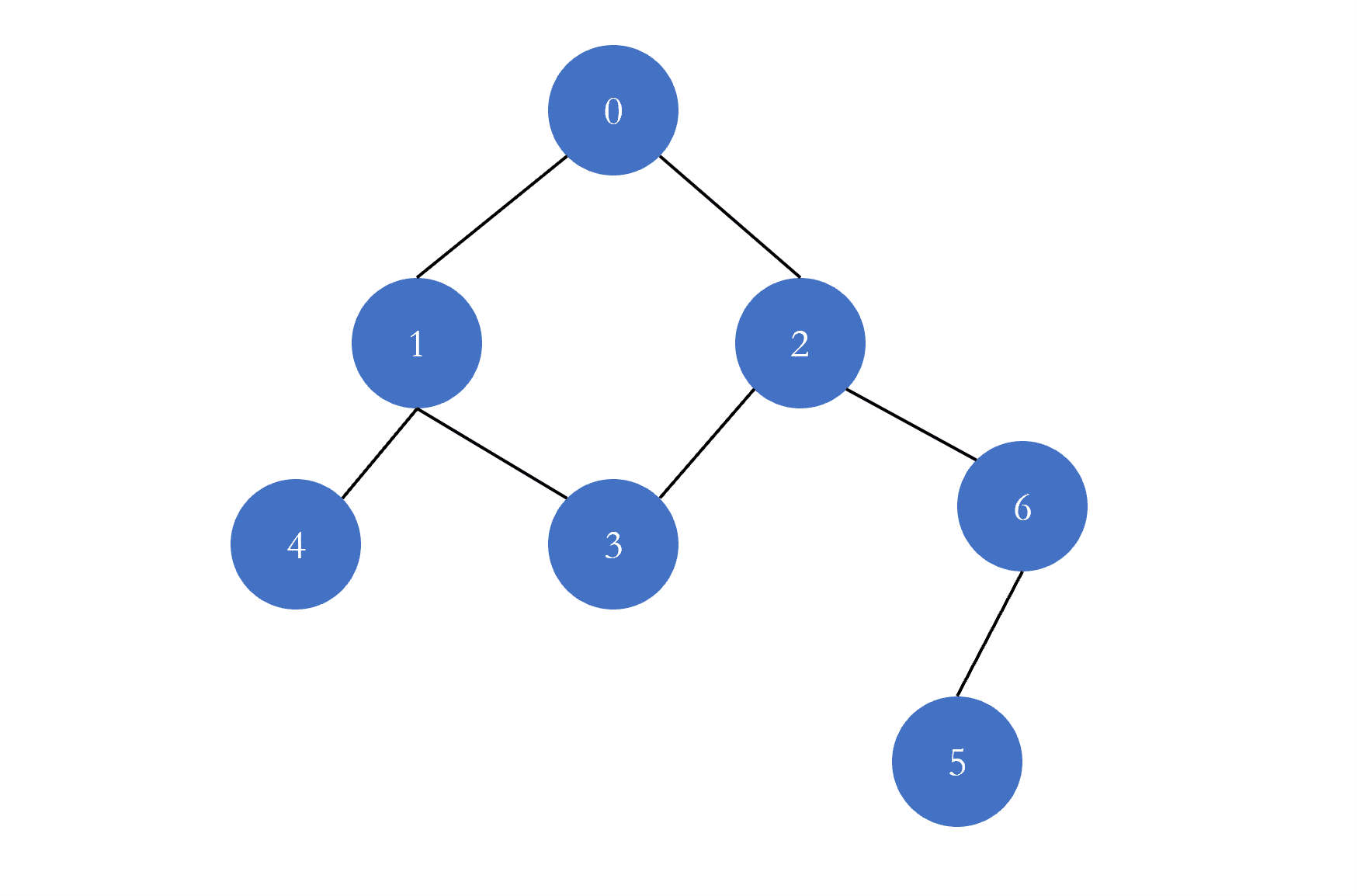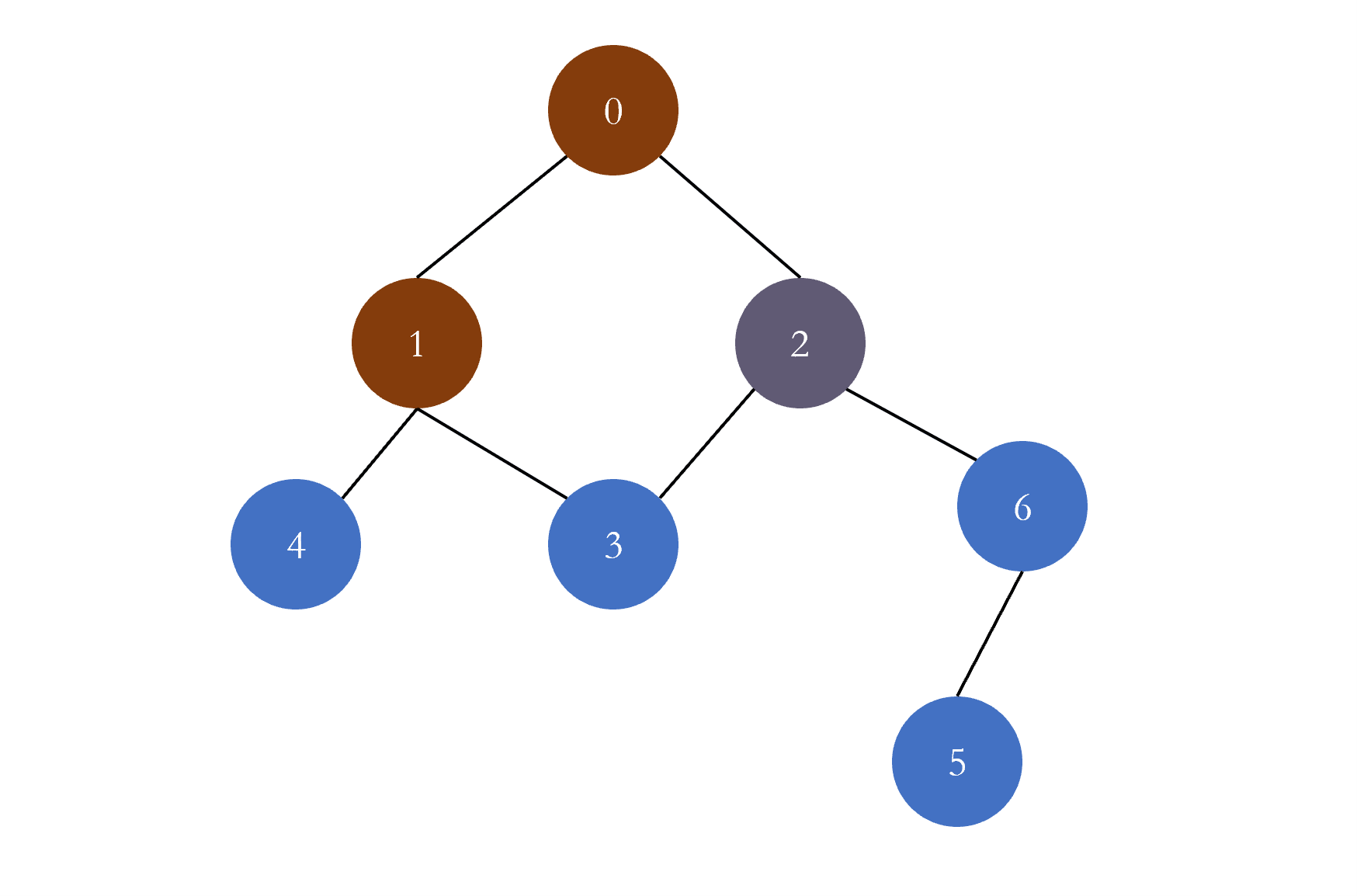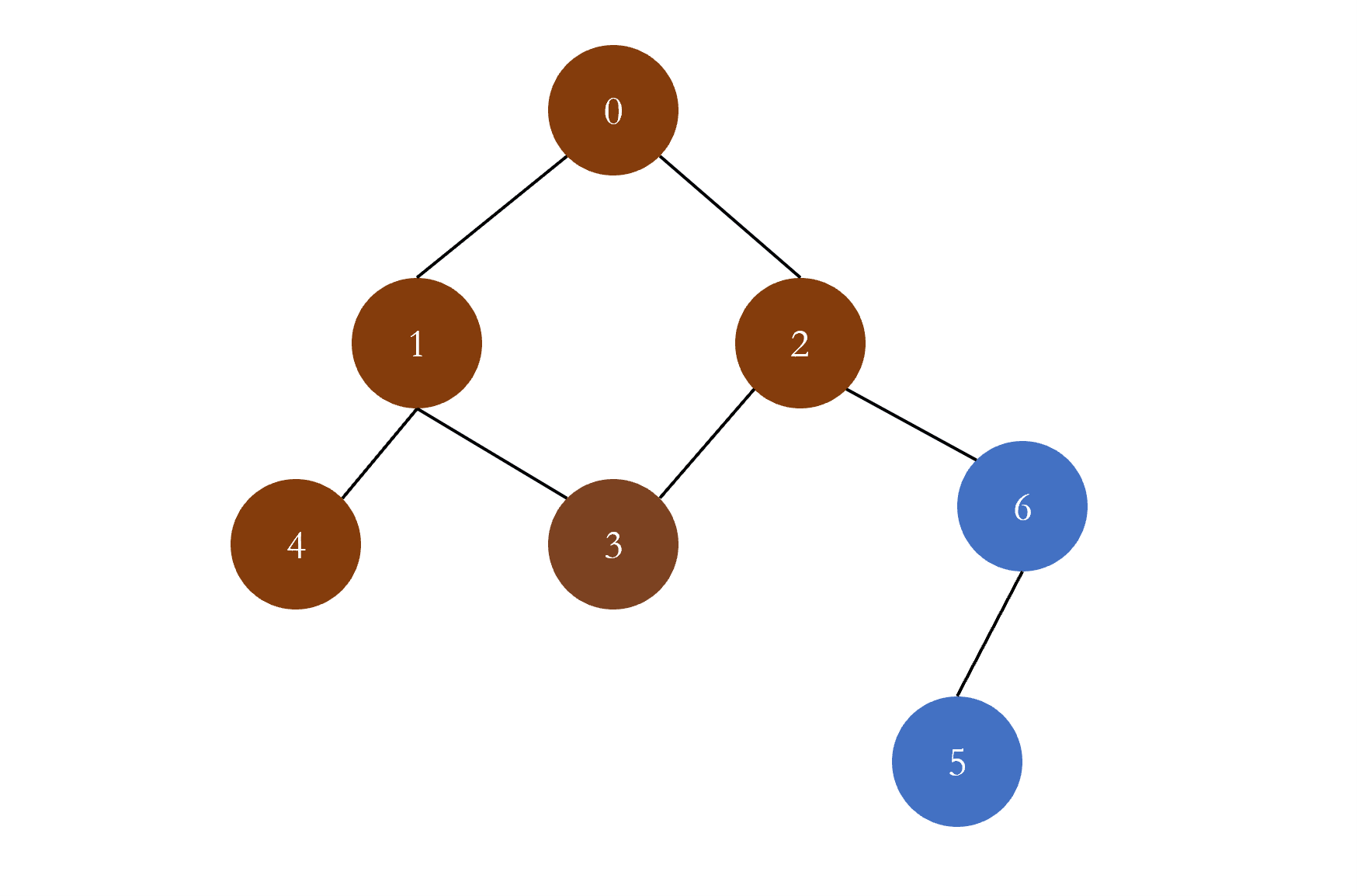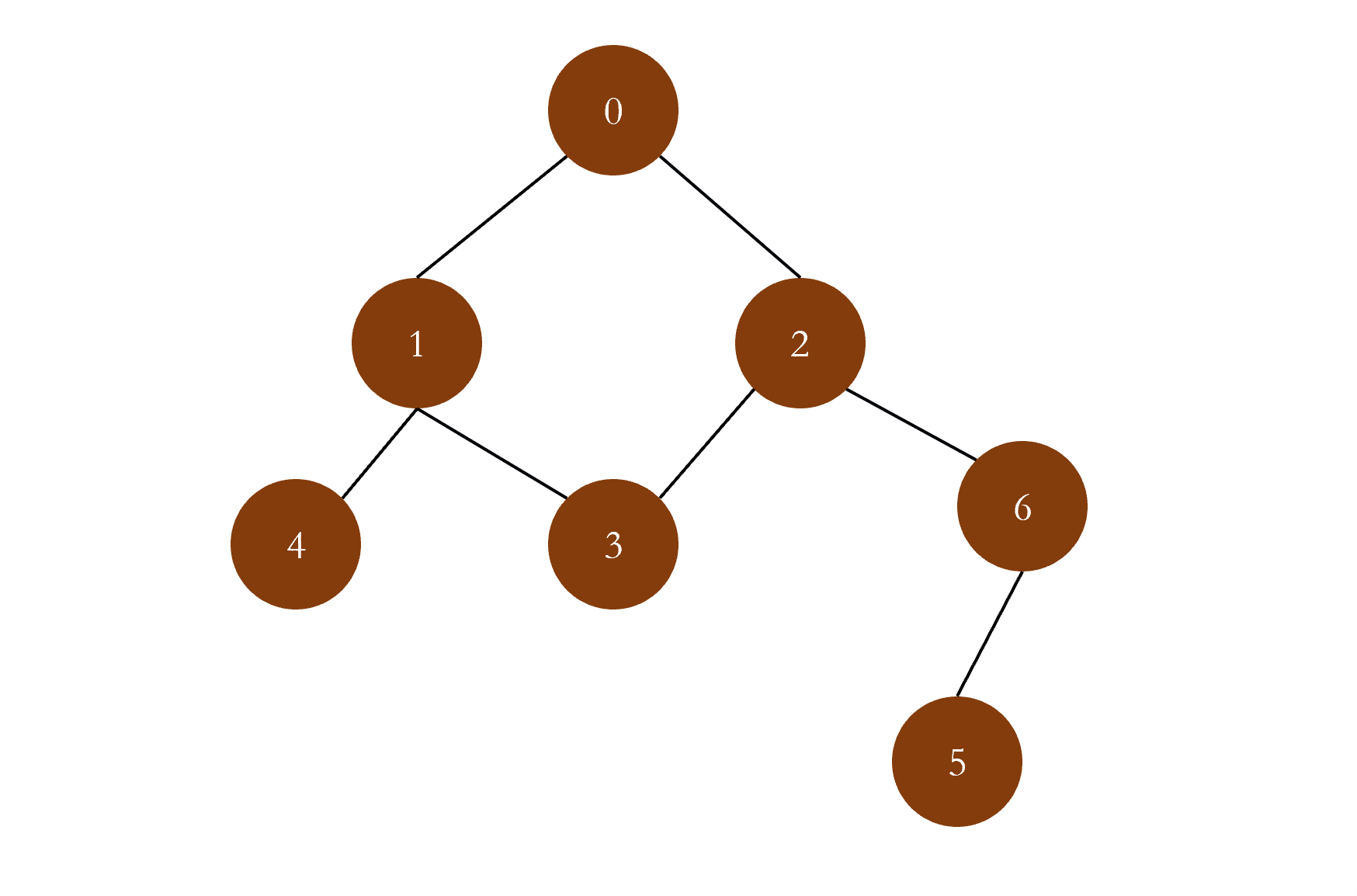
树的层序遍历

树的层序遍历是指一层一层的遍历树的节点，它的实现是借助于队列进行实现的：

每一次从队列的头部取出元素进行遍历，然后将该元素的左右孩子添加进队列，以此往复，直至队列为空，遍历结束。

import java.util.LinkedList;
import java.util.Queue;

public class BinaryTree {
    private class Node {
        private Node left;
        private Node right;
        private int value;
        
        public Node(int value) {
            this.value = value;
        }
    }
    
    private Node root;
    
    public BinaryTree(int value) {
        root = new Node(value);
    }
    
    public void levelOrder() {
        if (root == null) {
            return;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            Node node = queue.remove();
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
            System.out.println(node.value);
        }
    }
}

图的广度遍历

图的广度优先遍历与树的层序遍历相似，所谓的广度是指尽可能的遍历所有的相邻元素

广度优先遍历的实现同树的层序遍历类似，也是借助于队列这种数据结构，每次从队列的头部取出节点进行遍历，然后将该节点的所有相邻节点添加进队列，但是需要注意的是，因为图有可能发生重复遍历，所以需要使用visited 标记已遍历的节点；另外还需要考虑到有多个联通分量的情况，与深度优先遍历的写法类似

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;

public class BFSGraph {

    private Graph graph;
    private boolean[] visited;
    private ArrayList<Integer> order;

    public BFSGraph(Graph graph) {
        this.graph = graph;
        visited = new boolean[graph.V()];
        order = new ArrayList<>(graph.V());

        for (int i = 0; i < graph.V(); i++) {
            if (!visited[i]) {
                bfs(i);
            }
        }
    }

    private void bfs(int s) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(s);
        visited[s] = true;
        while (!queue.isEmpty()) {
            int v = queue.remove();
            order.add(v);
            for (int w: graph.adj(v)) {
                if (!visited[w]) {
                    queue.add(w);
                    visited[w] = true;
                }
            }
        }
    }

    public static void main(String[] args) {
        Graph graph = new AdjSet("g4.txt");
        BFSGraph bfsGraph = new BFSGraph(graph);
        System.out.println(bfsGraph.order);
    }
}

单源路径问题

对于路径问题的思路同DFS，使用一个 pre 数组，保存当前节点的上一个节点，当查询源节点到某个目的节点的路径时，只要从目的节点根据 pre 数组一直查找它的前一个节点，直到前一个节点为源节点就找到了路径

import java.util.*;

public class SingleSourcePath {
    private Graph graph;
    private int s;

    private boolean[] visited;
    private int[] pre;

    public SingleSourcePath(Graph graph, int s) {
        this.graph = graph;
        this.s = s;

        visited = new boolean[graph.V()];
        pre = new int[graph.V()];

        Arrays.fill(visited, false);
        Arrays.fill(pre, -1);

        bfs(s);
    }

    private void bfs(int s) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(s);
        visited[s] = true;
        pre[s] = s;

        while (!queue.isEmpty()) {
            int v = queue.remove();
            for (int w: graph.adj(v)) {
                if (!visited[w]) {
                    queue.add(w);
                    visited[w] = true;
                    pre[w] = v;
                }
            }
        }
    }

    private void validate(int v) {
        if (v < 0 || v >= graph.V()) {
            throw new IllegalArgumentException("v is out of index");
        }
    }

    public boolean isConnected(int t) {
        validate(t);
        return visited[t];
    }

    public ArrayList<Integer> path(int t) {
        ArrayList<Integer> res = new ArrayList<>();
        if (!isConnected(t)) {
            return res;
        }

        int cur = t;
        while (cur != s) {
            res.add(cur);
            cur = pre[cur];
        }
        res.add(s);

        Collections.reverse(res);
        return res;
    }

    public static void main(String[] args) {
        Graph graph = new AdjSet("g4.txt");
        SingleSourcePath singleSourcePath = new SingleSourcePath(graph, 0);
        // 0 -> 6: [0, 2, 6]
        System.out.println("0 -> 6: " + singleSourcePath.path(6));
    }
}

对于同样的图，使用深度优先遍历，结果是

0 -> 6: [0, 1, 3, 2, 6]

BFS 找到的路径比 DFS 找到的路径要短，这不是巧合，因为在无向无环图中，BFS 有一个重要的性质就是它寻找到的路径是最短路径，或者说经历的节点最少。为什么? 换种角度看，广度优先遍历是按照距离源的最小距离遍历的。

下面一个问题是寻找源到各点之间的距离，这个最简单的实现就是获得源到各点之间的路径，然后获得路径的长度即可推算出距离。下面提供一种更快的方法，无须先获得路径。首先我们需要声明一个 dis 数组来保存源到各点的距离，假设 w 是 v 的相邻节点，且 v 先被遍历，那么 s -> w 的距离为 s -> v + 1，即 dis[w] = dis[v] + 1

import java.util.*;

public class SingleSourcePath {
    private Graph graph;
    private int s;

    private boolean[] visited;
    private int[] pre;
    // dis 数组保存源到各节点的距离
    private int[] dis;

    public SingleSourcePath(Graph graph, int s) {
        this.graph = graph;
        this.s = s;

        visited = new boolean[graph.V()];
        pre = new int[graph.V()];
        // 初始化
        dis = new int[graph.V()];

        Arrays.fill(visited, false);
        Arrays.fill(pre, -1);
        // 初始化
        Arrays.fill(dis, -1);

        bfs(s);
    }

    private void bfs(int s) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(s);
        visited[s] = true;
        pre[s] = s;
        // 源到源的距离为 0
        dis[s] = 0;

        while (!queue.isEmpty()) {
            int v = queue.remove();
            for (int w: graph.adj(v)) {
                if (!visited[w]) {
                    queue.add(w);
                    visited[w] = true;
                    pre[w] = v;
                    // 更新 dis
                    dis[w] = dis[v] + 1;
                }
            }
        }
    }
    
    // 与 path 相关代码省略
    public int dis(int t) {
        validate(t);
        return dis[t];
    }
}