图

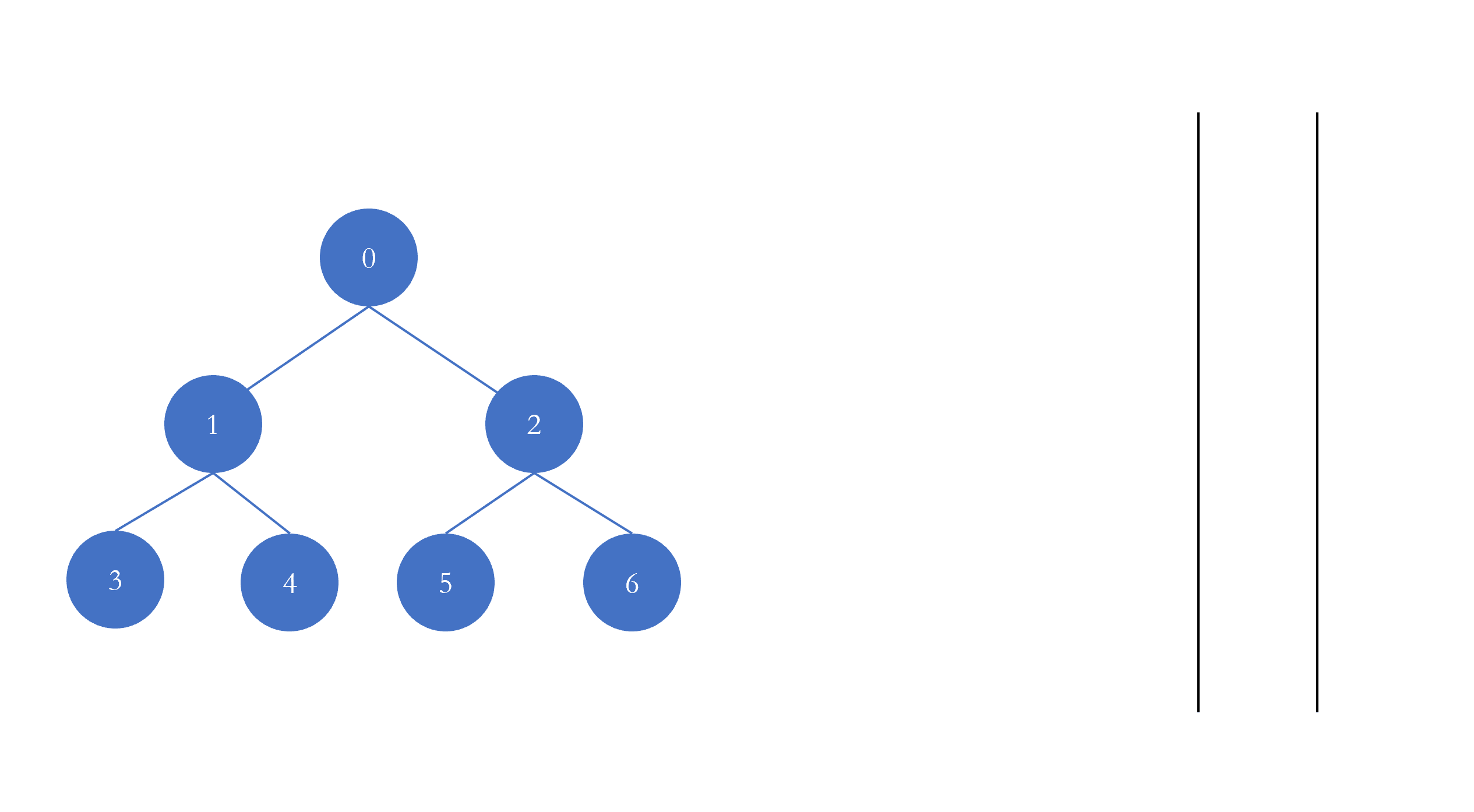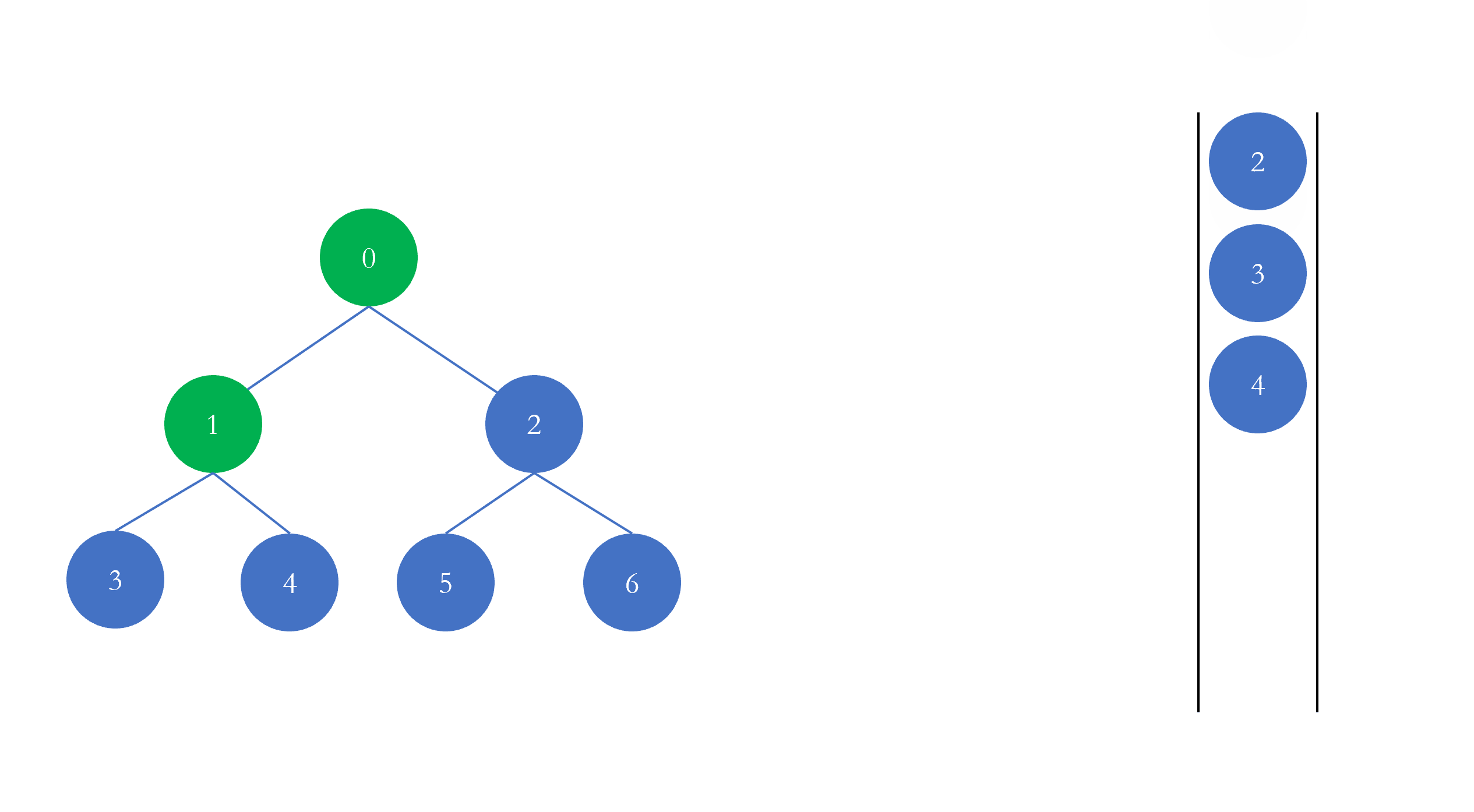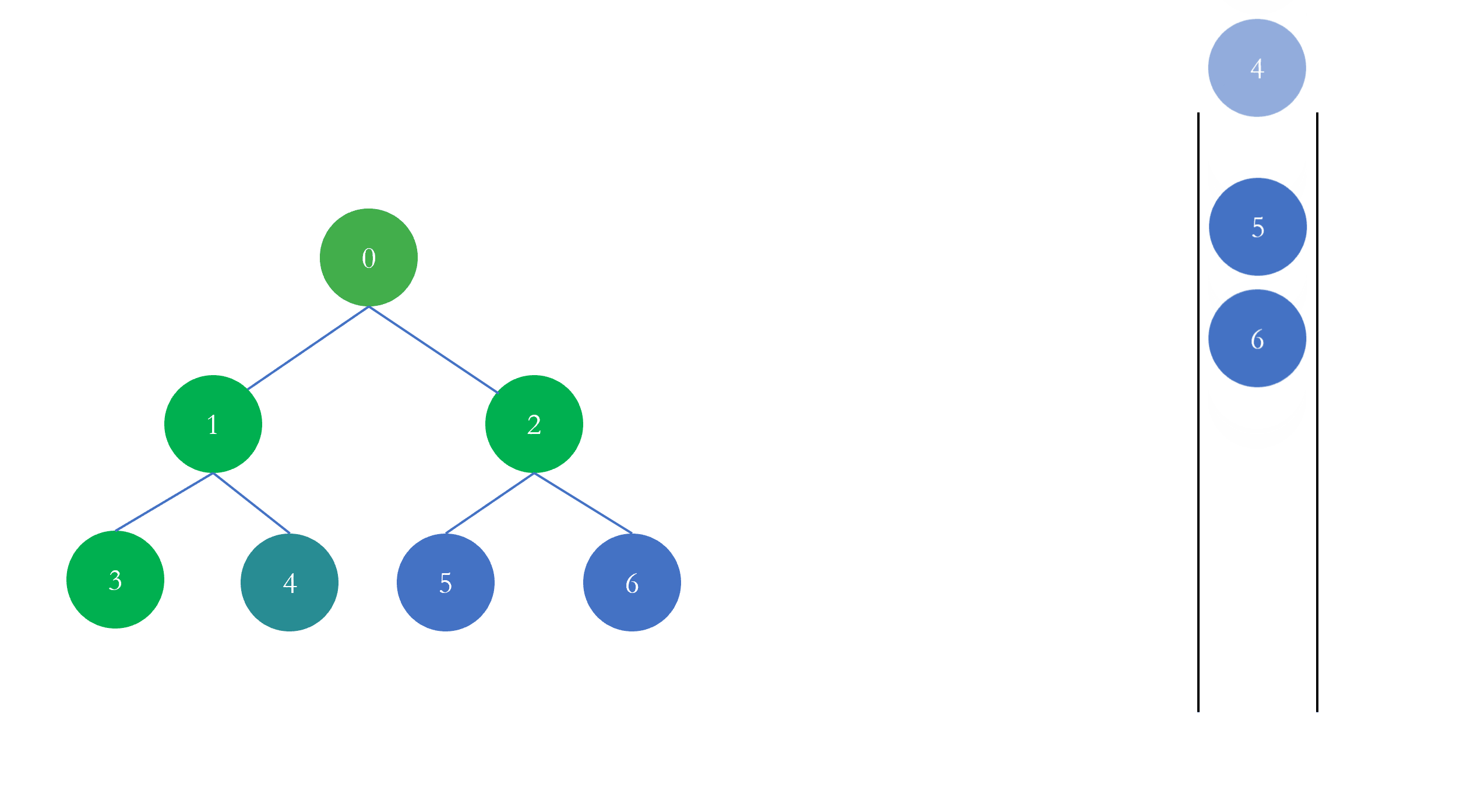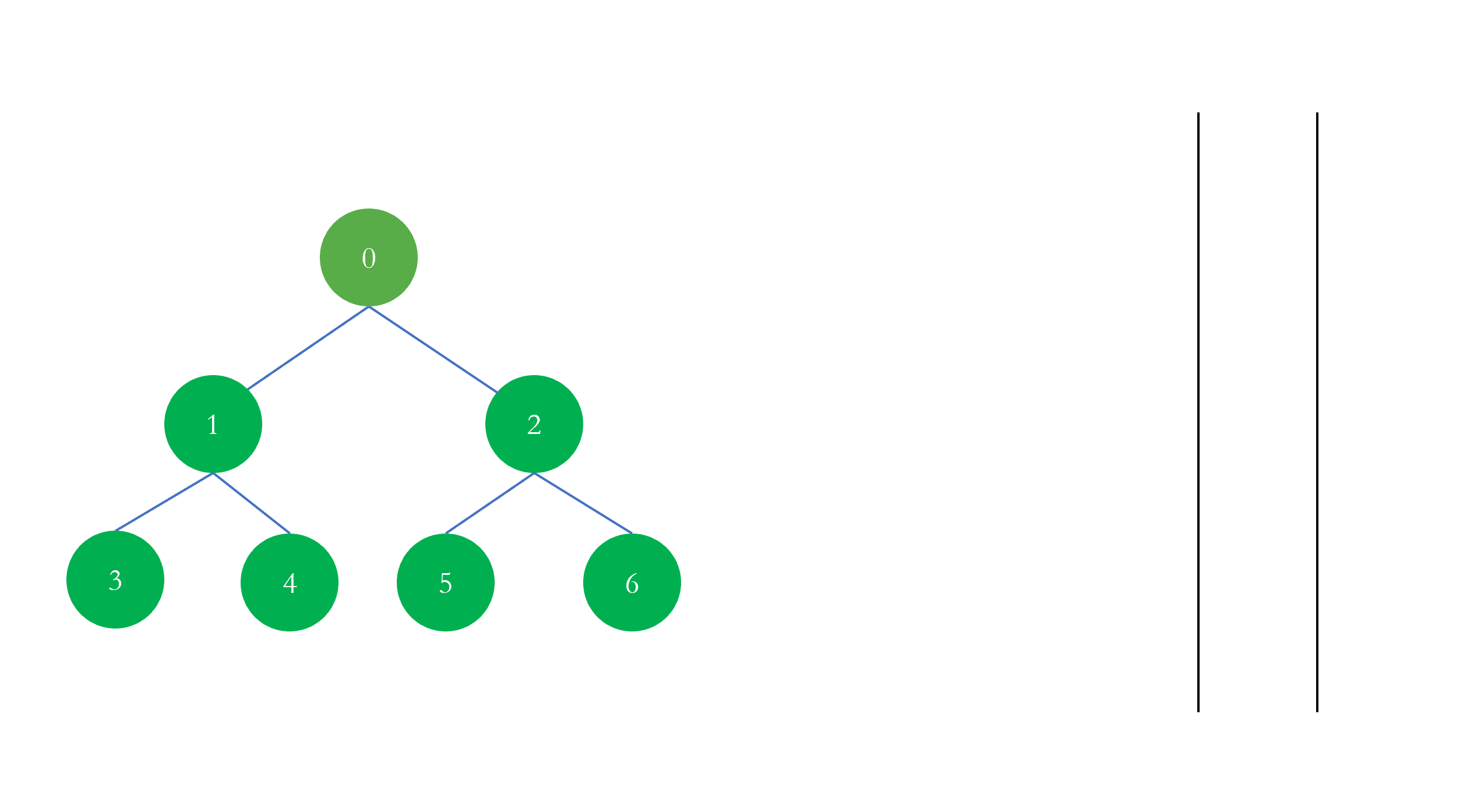
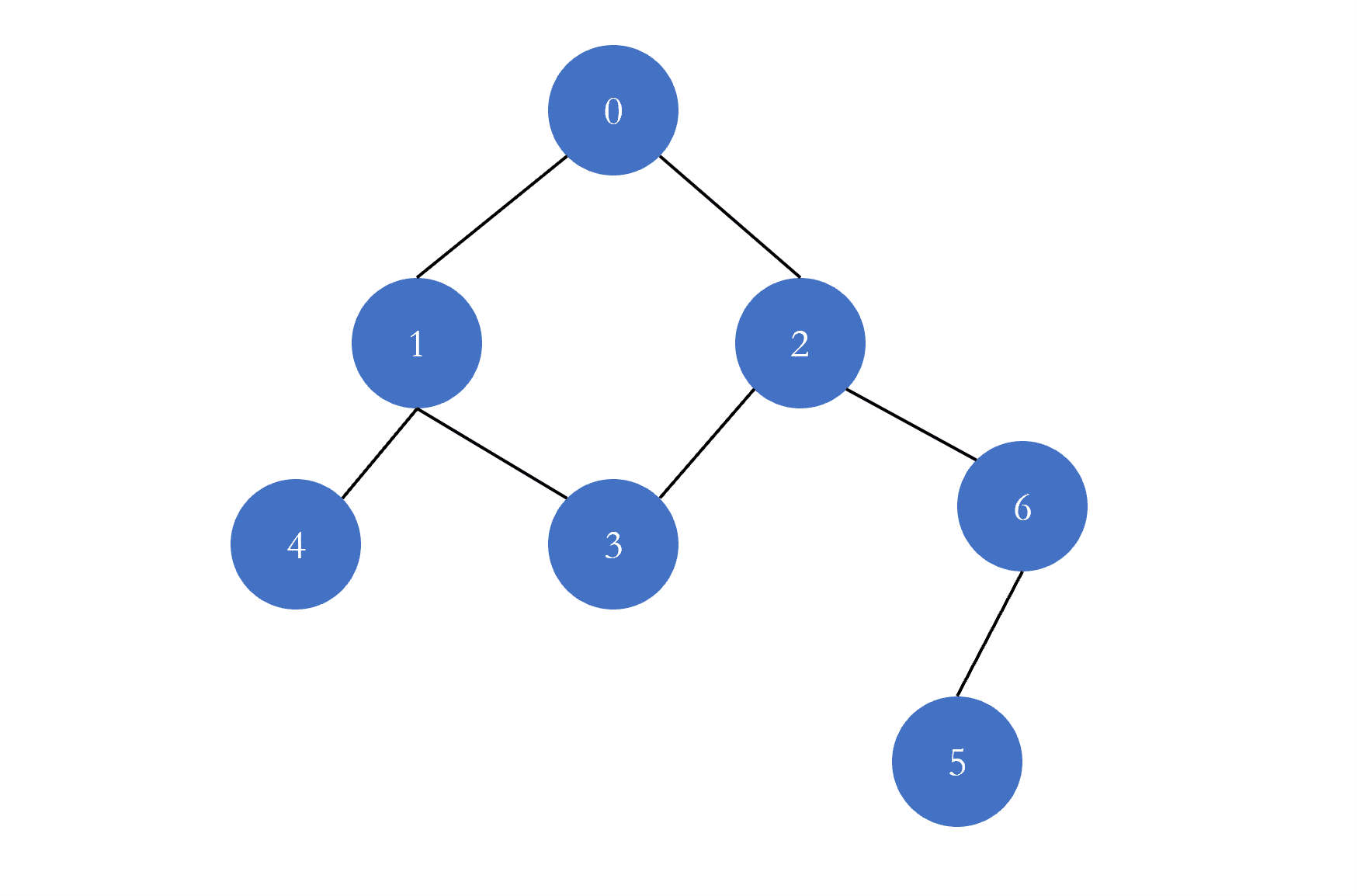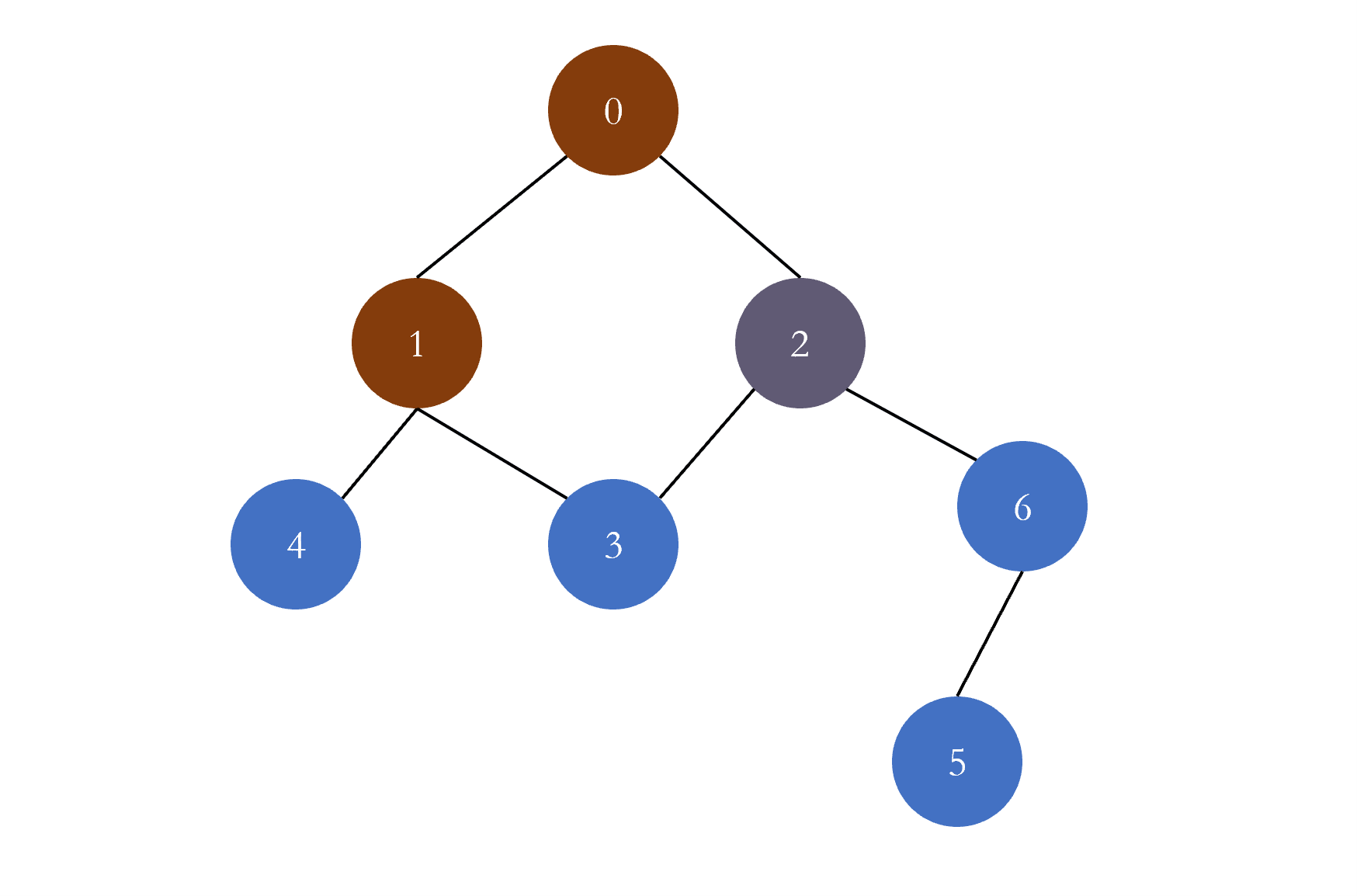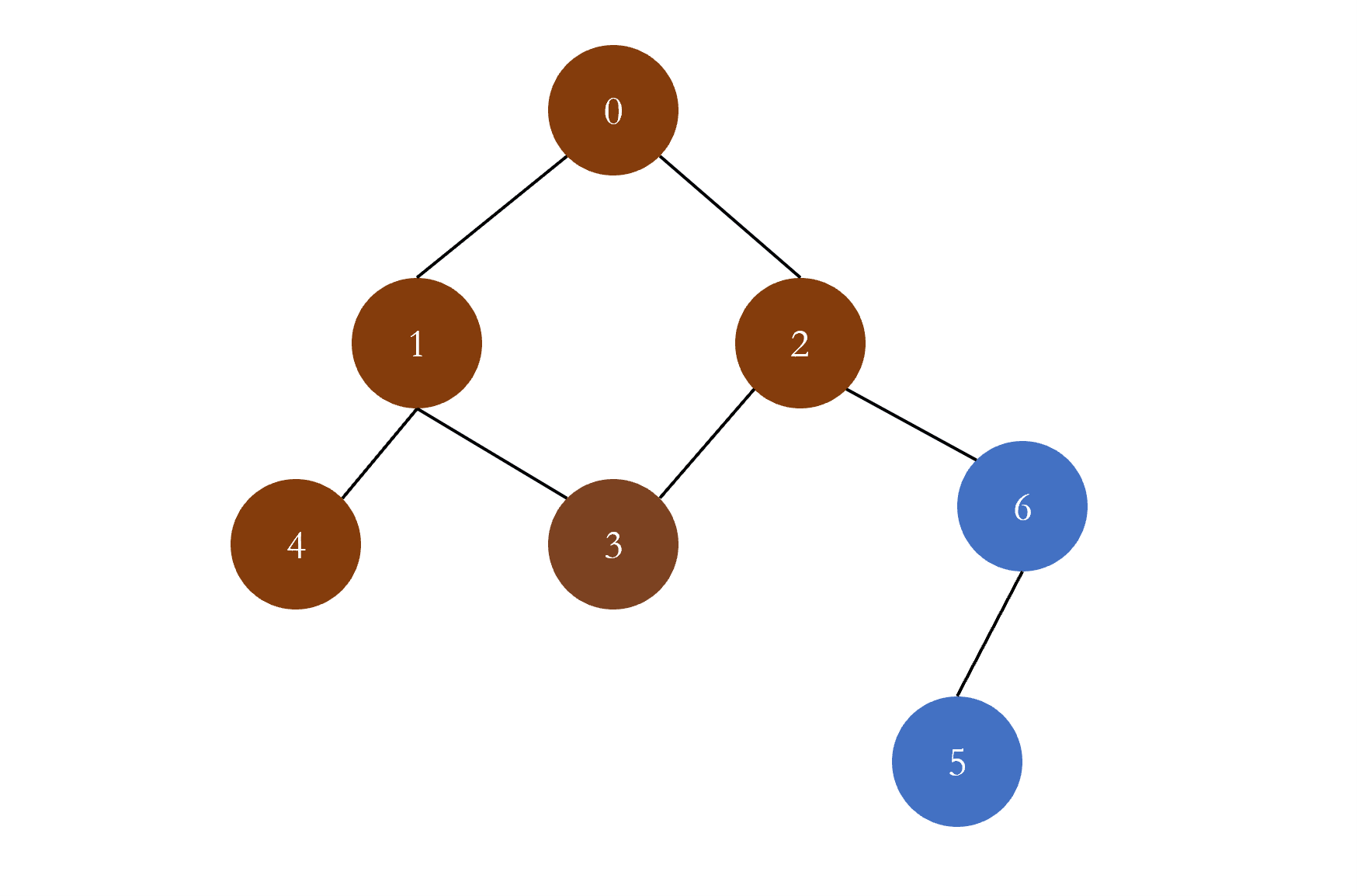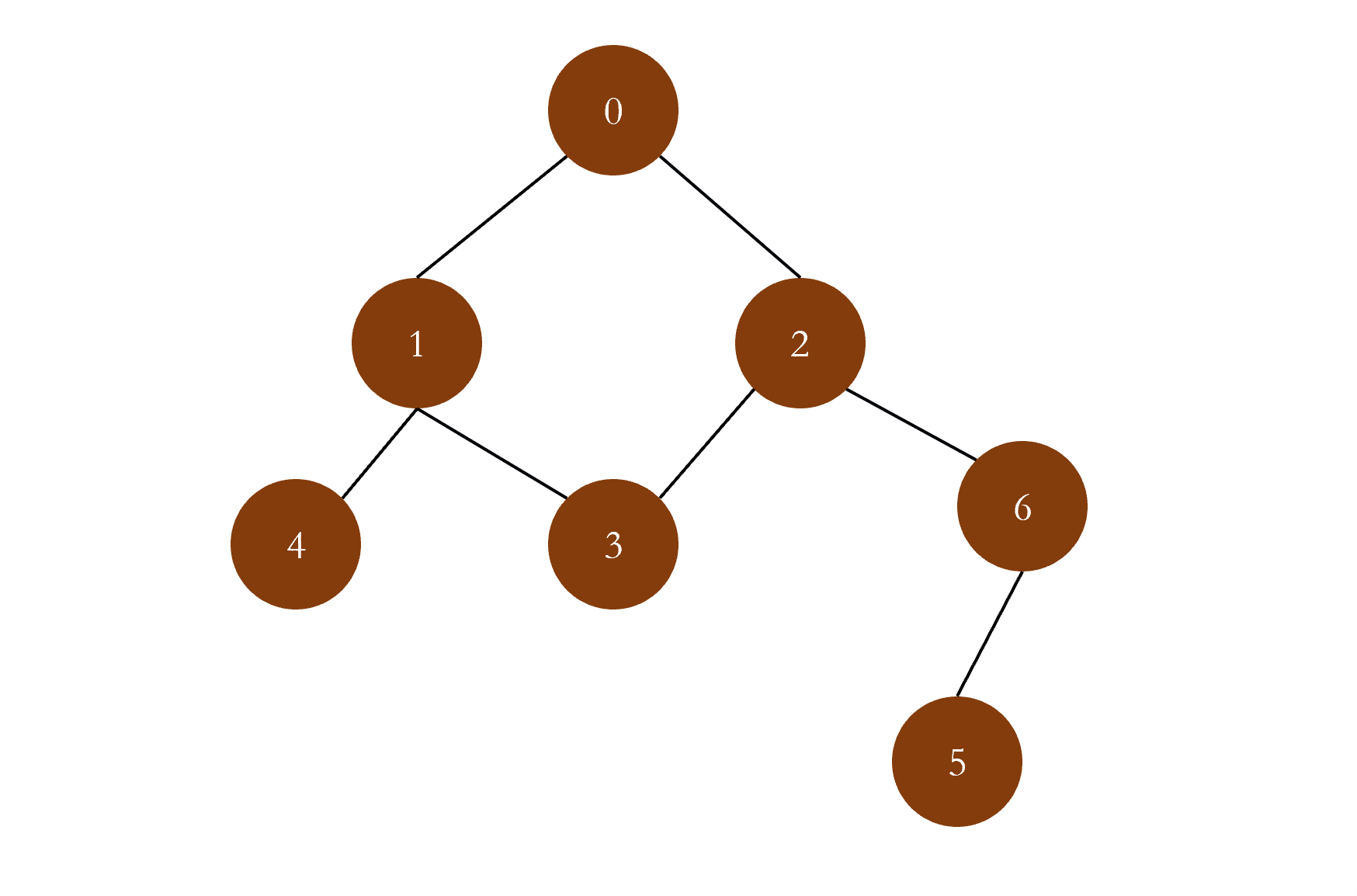
图的表示

首先我们来看看图的数据结构长什么样子

一个图它由顶点 Vertex 和边 Edge 组成，上图蓝色的节点表示顶点，而节点与节点之间的有条线连着，这就是顶点之间的边。为了在计算机中表示图，我们给图的顶点编了号，从 $0$ 开始。在实际的模型中，顶点可能表示的是一个地铁站点，社交网络中的一个人，我们可以通过哈希表将编号与顶点实际的意义映射起来，进而把顶点的具体意义抽象为编号或者下标，当图的顶点以编号表示时，它就不具有具体的意义，从而我们可以研究图的一般理论，而当我们需要结论的具体意义时，可以通过哈希表将编号映射为具体的意义。

图的分类

根据边是否有方向可以分为有向图和无向图，根据边上有否有权值可以分为有权图和无权图

	有向	无向
有权	有向有权图	无向有权图
无权	有向无权图	无向无权图

图的基本概念

在进入正题之前，简单的介绍一下在后面会遇到的关于图的基本概念。

• 自环边：图中有一个顶点有条边指向自己
• 平行边：两个顶点之间有两条边

如果一幅图既没有自环边，也没有平行边，我们就称该图为简单图。我们只处理简单图，如果图中有自环边或者平行边，我们会忽略这种边，或者抛出异常。

在一个图中，并不是所有的顶点都是联通的，如下

例如顶点 6-7 和顶点 0-5 之间是不联通的，像上面这样的图，我们认为它有两个联通分量，顶点 0-5 和顶点 6-7 分别代表一个联通分量。

另外，根据图中是否有环，我们可以将图分为有环图和无环图

最后介绍一个有关图的概念，那就是度(degree)，对于无向图和有向图，度的定义是不同的，这里我们介绍无向图关于度的定义，度指的是某个顶点有多少个邻边，度是顶点的属性。比如对于下图

顶点 $0$ 的度为 $2$，因为顶点 $0$ 有两个邻边，同理，顶点 $2$ 的度为 $3$，因为它有三个邻边。

图的表示

所谓图的表示，就是指如何在计算机中保存一个图的数据结构

如上图，怎么将它保存在计算机中。如果学习过其他数据结构的话，如栈，队列，树，它们是怎么表示的呢?

对于栈和队列这种线性的数据结构，我们一般使用数组或者链表来进行存储，而对于树这种数据结构，我们一般使用链表进行表示，每个节点都有两个指针分别指向它的左孩子和右孩子，当然对于某些树结构，如堆、线段树，我们也可以使用数组来进行表示，因为这两种数据结构都是满二叉树，它们的孩子节点与父节点之间含有某种关系，可以十分方便的使用数组进行表示。

邻接矩阵

首先我们介绍使用一个矩阵来存储图，如果整个图有 $V$ 个节点，那么我们就用 $V \times V$ 大小的矩阵来存储图，假设这个矩阵记做 $A$，如果 $A[i][j] = 1$，则说明顶点 $i$ 与顶点 $j$ 之间存在一条边，反之如果 $A[i][j] = 0$，则说明顶点 $i$ 与顶点 $j$ 之间不存在一条边

因为不存在自环边，所以 $A[i][i]$ 的值一定为 $0$，即矩阵对角线上的值一定是 $0$。

在构建一张图时，我们会读取一个 txt 的文件，根据这个文件我们使用矩阵来存储一张图，例如上图所对应的 txt 内容如下

6 7
0 1
0 2
1 3
2 3
2 4
3 5
4 5

这个 txt 表示什么意思呢? 第一行的两个数字表示图中的顶点数和边数，如上图有 $6$ 个顶点和 $7$ 条边，后面每行的两个数字表示两个顶点，表示这两个顶点之间存在一条边，如第二行就表示顶点 $0$ 和顶点 $1$ 之间存在一条边，因为总共有 $7$ 条边，所以第一行后应该有 $7$ 行表示有 $7$ 条边。

代码如下：

import java.io.File;
import java.io.FileNotFoundException;
import java.util.Scanner;

public class AdjMatrix {
    // 图的边数
    private int E;
    // 图的顶点个数
    private int V;
    // 表示图的矩阵
    private int[][] matrix;

    public AdjMatrix(String filename) {
        // 从文件中读取图的数据
        File file = new File(filename);
        Scanner scanner = null;
        try {
            // 第一行是顶点数和边数
            scanner = new Scanner(file);
            this.V = scanner.nextInt();
            matrix = new int[this.V][this.V];
            this.E = scanner.nextInt();
            
            for (int i = 0; i < this.E; i++) {
                // 读取两个相邻的顶点
                int a = scanner.nextInt();
                int b = scanner.nextInt();

                // 设置为 1 表示相邻
                this.matrix[a][b] = 1;
                this.matrix[b][a] = 1;
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        } finally {
            assert scanner != null;
            scanner.close();
        }
    }

    // 当打印对象时，将矩阵打印出来
    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder();
        stringBuilder.append(String.format("V: %d, E: %d\n", this.V, this.E));
        for (int i = 0; i < this.V; i++) {
            for (int j = 0; j < this.V; j++) {
                stringBuilder.append(String.format("%d ", this.matrix[i][j]));
            }
            stringBuilder.append("\n");
        }
        return stringBuilder.toString();
    }

    public static void main(String[] args) {
        AdjMatrix adjMatrix = new AdjMatrix("g.txt");
        System.out.println(adjMatrix);
    }
}

打印结果为

V: 6, E: 7
0 1 1 0 0 0 
1 0 0 1 0 0 
1 0 0 1 1 0 
0 1 1 0 0 1 
0 0 1 0 0 1 
0 0 0 1 1 0

AdjMatrix 类有三个属性

属性	含义
V	表示顶点数
E	表示边数
matrix	表示图的矩阵

但是上面的程序还不够健壮，因为我们没有对 g.txt 中读到的数字进行校验，例如读到的顶点个数为负数，读到的顶点编号不合理，例如有 $5$ 个顶点，但是它的编号为 $10$。另外，我们只处理简单图，对于自环边以及平行边也没有进行处理，所以我们需要对上面的代码进行改进

import java.io.File;
import java.io.FileNotFoundException;
import java.util.ArrayList;
import java.util.Scanner;

public class AdjMatrix {
    private int E;
    private int V;
    private int[][] matrix;

    public AdjMatrix(String filename) {
        File file = new File(filename);
        Scanner scanner = null;
        try {
            scanner = new Scanner(file);
            
            // 如果读取到的 V 和 E 小于 0，那么抛出异常
            this.V = scanner.nextInt();
            if (this.V < 0) {
                throw new IllegalArgumentException("V Must Be Positive");
            }
            matrix = new int[this.V][this.V];
            this.E = scanner.nextInt();
            if (this.E < 0) {
                throw new IllegalArgumentException("E Must Be Positive");
            }

            for (int i = 0; i < this.E; i++) {
                // 对读取到的顶点编号进行验证，是否在 [0, V) 的范围中
                int a = scanner.nextInt();
                validateVertex(a);
                int b = scanner.nextInt();
                validateVertex(b);

                // 如果存在自环边，抛出异常
                if (a == b) {
                    throw new IllegalArgumentException("Self loop exists");
                }
                // 如果存在平行边，抛出异常
                if (this.matrix[a][b] == 1) {
                    throw new IllegalArgumentException("Parallel edge exists");
                }
                this.matrix[a][b] = 1;
                this.matrix[b][a] = 1;
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        } finally {
            assert scanner != null;
            scanner.close();
        }
    }

    // 对顶点编号进行验证，是否合法
    private void validateVertex(int v) {
        if (v < 0 || v >= this.V) {
            throw new IllegalArgumentException("Vertex " + v + " is invalid");
        }
    }

    // 返回顶点数
    public int V() {
        return this.V;
    }

    // 返回边数
    public int E() {
        return this.E;
    }

    // 返回与顶点 v 相邻的所有顶点
    public ArrayList<Integer> adj(int v) {
        validateVertex(v);
        ArrayList<Integer> res = new ArrayList<>();
        for (int i = 0; i < this.V; i++) {
            if (this.matrix[v][i] == 1) {
                res.add(i);
            }
        }

        return res;
    }

    // 判断顶点 v 和 w 是否相邻
    public boolean hasEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return this.matrix[v][w] == 1;
    }

    // 返回顶点 v 的度，即与顶点 v 相邻的顶点的个数
    public int degree(int v) {
        return adj(v).size();
    }

    // toString 不变，节省篇幅，省略
}

在上面我们对读取到的数字都进行了检查，保证了代码的健壮性。除了增强了代码的健壮性以外，我们还在类中添加了五个方法，具体作用见下表

方法	作用
int V()	返回图的顶点数
int E()	返回图的边数
ArrayList adj(int v)	返回与顶点 v 相邻的顶点
boolean hasEdge(int v, int w)	判断两顶点是否相邻
int degree(int v)	返回顶点 v 的度

在最后我们分析一下使用邻接矩阵表示的空间复杂度和时间复杂度

空间复杂度：$O(V^2)$

时间复杂度：

• 建图：$O(E)$
• 获得与顶点 $v$ 相邻的顶点：$O(V)$
• 查看两个顶点是否相邻：$O(1)$

对于建图来说，因为我们必须扫描所有的边才能获得必要的信息，所以建图的时间复杂度最少也是 $O(E)$，无法再优化；而查看两个顶点是否相邻，时间复杂度为 $O(1)$，无需优化，那么我们看看空间复杂度和获得与顶点 $v$ 相邻的顶点的时间复杂度能否进行优化。

因为我们平常遇到的图都是稀疏图，所谓稀疏图就是一幅图它的度平均值对于图的节点数目来说很小，这就会导致我们的邻接矩阵是一个稀疏矩阵，即大部分的元素是 $0$。例如对于一个社交网络，有一亿个节点，但是对于每个人来说，他认识的人最多几百个，也就是这幅图平均的度为几百，相对于一亿来说十分的小，所以社交网络是一个稀疏图。

建立一个图，我们只需要知道一幅图的顶点信息以及边的信息即可，也就是说我们只需要 $O(V + E)$ 的空间复杂度就可以表示一幅图，对于稀疏图来说，由于图的每个顶点度的平均值远远小于节点数，而 $E$ 的大小等于平均度的值乘以节点数，即
$$
E = degree * V
$$
从而有
$$
degree \ll V \Rightarrow E \ll V^2
$$
得到
$$
O(V + E) \ll O(V^2)
$$
所以使用邻接矩阵表示图，对于稀疏矩阵来说，其实浪费了很多的空间，下面将介绍使用另一种方法表示图，无论是对于稀疏图还是稠密图，都可以有更好的性能。

邻接表

在这个小节中将讲解使用邻接表来表示矩阵，所谓的邻接表，是指对于每个顶点来说，我们使用一个链表来记录与它相邻的节点，如下图

图中表格第一列表示顶点编号，顶点编号后的一行表示与该顶点相邻的顶点，例如对于第一行，表示与顶点 $0$ 相邻的顶点有顶点 $1$ 和 $2$。

现在我们就要编码实现，因为大部分的逻辑与邻接矩阵是相同的，所以很多的代码与邻接矩阵表示的方式是一样的，不过因为底层保存图使用的是链表，有一些写法的不同，在下面的代码中我也会标出

import java.io.File;
import java.io.FileNotFoundException;
import java.util.LinkedList;
import java.util.Scanner;

public class AdjList {
    private int E;
    private int V;
    // 对每一个顶点，使用一个链表来存储与它相邻的顶点
    private LinkedList<Integer>[] lists;

    public AdjList(String filename) {
        File file = new File(filename);
        Scanner scanner = null;
        try {
            scanner = new Scanner(file);
            this.V = scanner.nextInt();
            if (this.V < 0) {
                throw new IllegalArgumentException("V Must Be Positive");
            }

            // 初始化链表
            this.lists = new LinkedList[this.V];
            for (int i = 0; i < this.V; i++) {
                this.lists[i] = new LinkedList<>();
            }

            this.E = scanner.nextInt();
            if (this.E < 0) {
                throw new IllegalArgumentException("E Must Be Positive");
            }

            for (int i = 0; i < this.E; i++) {
                int a = scanner.nextInt();
                validateVertex(a);
                int b = scanner.nextInt();
                validateVertex(b);

                if (a == b) {
                    throw new IllegalArgumentException("Self loop exists");
                }
                // 平行边的判断
                if (lists[a].contains(b)) {
                    throw new IllegalArgumentException("Parallel edge exists");
                }

                // 将相邻顶点添加到自己的链表中
                this.lists[a].add(b);
                this.lists[b].add(a);
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        } finally {
            assert scanner != null;
            scanner.close();
        }
    }

    private void validateVertex(int v) {
        if (v < 0 || v >= this.V) {
            throw new IllegalArgumentException("Vertex " + v + " is invalid");
        }
    }

    public int V() {
        return this.V;
    }

    public int E() {
        return this.E;
    }

    public LinkedList<Integer> adj(int v) {
        validateVertex(v);
        // 直接返回顶点自己的链表即可
        return lists[v];
    }

    public boolean hasEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return this.lists[v].contains(w);
    }

    public int degree(int v) {
        return adj(v).size();
    }
    
    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder();
        stringBuilder.append(String.format("V: %d, E: %d\n", this.V, this.E));
        for (int v = 0; v < this.V; v++) {
            stringBuilder.append(String.format("%d : ", v));
            for (int w: adj(v)) {
                stringBuilder.append(String.format("%d ", w));
            }
            stringBuilder.append("\n");
        }
        return stringBuilder.toString();
    }

    public static void main(String[] args) {
        AdjList adjList = new AdjList("g.txt");
        System.out.println(adjList);
    }
}

输出为

V: 6, E: 7
0 : 1 2 
1 : 0 3 
2 : 0 3 4 
3 : 1 2 5 
4 : 2 5 
5 : 3 4 

下面分析一下使用邻接表实现图的时间复杂度和空间复杂度：

• 空间复杂度：$O(V + E)$
• 时间复杂度：
  • 建表：$O(VE)$
  • 获得与顶点 $V$ 相邻的顶点：$O(degree)$
  • 判断两个顶点是否相邻：$O(degree)$

建表的时间复杂度为 $O(VE)$，是因为每次我们都要扫描一遍表判断是否有平行边，判断两个顶点是否相邻的时间复杂度为 $O(degree)$，是因为需要遍历表来判断两个顶点是否相邻。上面两个操作都比使用邻接矩阵实现图的操作更加的费时，都是因为查找的能力比较慢(在建图时需要查重判断是否有平行边，判断两个顶点是否相邻时也需要在链表中进行查找)，所以我们是否有办法可以提高查找表的速度。

说到查找速度，不得不说哈希表和红黑树，所以我们可以考虑使用 HashSet 或者 TreeSet 来替代上面的 LinkedList，以此来提高查找速度，二者查找的时间复杂度如下

数据结构	查找时间复杂度
HashSet	$O(1)$
TreeSet	$O(\log v)$

从时间复杂度上看，使用 HashSet 是更好的选择，但是 TreeSet 有一个优点那就是有序性，这会带来两个优点

• 复现我的代码时可以得到与我一致的结果(输出的顺序)
• 当我使用图片解释算法过程时，输出的结果可以与我演示的结果一致，可以更好的理解算法

所以这里我选择 TreeSet。我们新建一个 AdjSet 类，复制 AdjList 的代码，将其中所有的 LinkedList 改为 TreeSet 即可，如下

import java.io.File;
import java.io.FileNotFoundException;
import java.util.Scanner;
import java.util.TreeSet;

public class AdjSet {
    private int E;
    private int V;
    private TreeSet<Integer>[] sets;

    public AdjSet(String filename) {
        File file = new File(filename);
        Scanner scanner = null;
        try {
            scanner = new Scanner(file);
            this.V = scanner.nextInt();
            if (this.V < 0) {
                throw new IllegalArgumentException("V Must Be Positive");
            }

            // 初始化链表
            this.sets = new TreeSet[this.V];
            for (int i = 0; i < this.V; i++) {
                this.sets[i] = new TreeSet<>();
            }

            this.E = scanner.nextInt();
            if (this.E < 0) {
                throw new IllegalArgumentException("E Must Be Positive");
            }

            for (int i = 0; i < this.E; i++) {
                int a = scanner.nextInt();
                validateVertex(a);
                int b = scanner.nextInt();
                validateVertex(b);

                if (a == b) {
                    throw new IllegalArgumentException("Self loop exists");
                }
                // 平行边的判断
                if (sets[a].contains(b)) {
                    throw new IllegalArgumentException("Parallel edge exists");
                }

                // 将相邻顶点添加到自己的链表中
                this.sets[a].add(b);
                this.sets[b].add(a);
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        } finally {
            assert scanner != null;
            scanner.close();
        }
    }

    private void validateVertex(int v) {
        if (v < 0 || v >= this.V) {
            throw new IllegalArgumentException("Vertex " + v + " is invalid");
        }
    }

    public int V() {
        return this.V;
    }

    public int E() {
        return this.E;
    }

    public TreeSet<Integer> adj(int v) {
        validateVertex(v);

        // 直接返回自己的链表即可
        return sets[v];
    }

    public boolean hasEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return this.sets[v].contains(w);
    }

    public int degree(int v) {
        return adj(v).size();
    }

    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder();
        stringBuilder.append(String.format("V: %d, E: %d\n", this.V, this.E));
        for (int v = 0; v < this.V; v++) {
            stringBuilder.append(String.format("%d : ", v));
            for (int w: adj(v)) {
                stringBuilder.append(String.format("%d ", w));
            }
            stringBuilder.append("\n");
        }
        return stringBuilder.toString();
    }

    public static void main(String[] args) {
        AdjSet adjSet = new AdjSet("g.txt");
        System.out.println(adjSet);
    }
}

在最后我们做一个改进，观察三个类的 adj 方法

// AdjMatrix
public ArrayList<Integer> adj(int v) {
    validateVertex(v);
    ArrayList<Integer> res = new ArrayList<>();
    for (int i = 0; i < this.V; i++) {
        if (this.matrix[v][i] == 1) {
            res.add(i);
        }
    }

    return res;
}

// AdjList
public LinkedList<Integer> adj(int v) {
    validateVertex(v);
    return lists[v];
}

// AdjSet
public TreeSet<Integer> adj(int v) {
    validateVertex(v);
    return sets[v];
}

这三个方法的返回值都不相同，这就会给使用者带来负担，它还需要记住每个类的返回值是什么，考虑到使用者拿到与顶点 $v$ 相邻的所有顶点，一般都是用来遍历，所以我们返回一个接口 Iterable，ArrayList LinkedList TreeSet 三个类都实现了该接口，如下

// AdjSet 其它两个类做相同修改
public Iterable<Integer> adj(int v) {
    validateVertex(v);
    return sets[v];
}

注意：记得还有修改 degree 方法，因为这是 adj 方法返回的是 Iterable 接口，该接口没有 size 方法，修改如下

public int degree(int v) {
 validateVertex(v);
 return this.sets[v].size();
}

其它两个类做类似的修改。

总结

在文章的最后，我们比较一下三种方法的空间复杂度和时间复杂度

	空间	建图时间	两顶点是否相邻	查找顶点的邻边
邻接矩阵	$O(V^2)$	$O(E)$	$O(1)$	$O(V)$
邻接表(LinkedList)	$O(V + E)$	$O(EV)$	$O(degree)$	$O(degree)$
邻接表(TreeSet)	$O(V + E)$	$O(E\log V)$	$O(\log degree)$	$O(degree)$

由上可见，底层使用 TreeSet 的邻接表来表示图，从空间和时间上都非常的优秀，在后面的文章，都将使用 TreeSet 版本的邻接表来表示图。

后面为了屏蔽差异，我们定义一个 Graph 的接口，这三个类都实现 Graph 接口，Graph 接口如下

public interface Graph {
 int V();
 int E();
 int degree(int v);
 boolean hasEdge(int v, int w);
 Iterable<Integer> adj(int v);
}

图的深度优先遍历

所谓图的遍历就是按照某种顺序访问图中所有的节点，根据访问的顺序不同，可以分为两类：

• 深度优先遍历
• 广度优先遍历

在本节中讲解深度优先遍历。

所谓深度优先遍历(Depth First Search，简称 DFS)，是指在遍历时，尽可能深的访问图的节点。为了更好的理解图的深度优先遍历，我们先看看树的深度优先遍历，与图的深度优先遍历一样，树的深度优先遍历也是指尽可能深的访问树的节点，也就是说如果一个节点有孩子节点，那么我们下一步就应该遍历它的孩子节点(深度)，如下

从上面的动图可以看出，当我们遍历完当前节点以后，如果该节点有孩子节点，那么接下来我们去遍历孩子节点，我们的遍历策略就是尽可能深的遍历。类比于图，对于图来说，如果一个图的节点有邻接节点，那么在遍历完该节点后，我们下一步就去遍历它的邻接节点

这就是图的深度优先遍历，上图深度优先遍历访问的顺序是 $[0, 1, 3, 2, 4, 5]$，我们将在下面的编程中验证是否正确。

图的遍历与树的遍历有一处不同，那就是重复访问问题。树不会发生重复访问的问题，这是因为树的节点只能通过父节点访问到，只有一种路径到达该节点，所以我们不必担心；但是对于图来说，一个图中的节点可以与多个节点进行连接，这就意味着有多种路径到达该节点，这就会导致某节点已经通过一个相邻的节点被访问，但是它还是有可能通过别的相邻节点再次被访问。

所以我们需要通过一个标志来表示某个图的节点是否已经被访问过了，如果已经被访问过了，那么我们就不能再次访问，我们通过一个 visited 数组来表示图中的某个节点是否已经被访问过了，visited 数组是一个 boolean 类型的数组，值为 true 时就表示该节点已经被访问过了，例如 visited[0] = true 就表示节点 0 已经被访问过了。

下面我就将编程具体实现：

import java.util.ArrayList;
import java.util.Arrays;

public class DFSGraph {
    // 图的表示中定义的 Graph 接口
    private Graph graph;
    // 保存深度优先遍历的顺序
    private ArrayList<Integer> order;
    // 保存节点是否已经被访问过
    private boolean[] visited;

    public DFSGraph(Graph graph) {
        this.graph = graph;
        order = new ArrayList<>(graph.V());
        // 初始化 visited 中的元素值为 false
        visited = new boolean[graph.V()];
        Arrays.fill(visited, false);
    }

    // DFS 的实现，首先从节点 0 开始遍历
    public void dfs() {
        dfs(0);
    }

    private void dfs(int v) {
        // 标记当前节点为访问过的状态
        visited[v] = true;
        // 向 order 中添加当前节点
        order.add(v);
        
        for (int w: graph.adj(v)) {
            // 如果邻接节点没有被访问过，那么遍历该邻接节点
            if (!visited[w]) {
                dfs(w);
            }
        }
    }
    
    public Iterable<Integer> order() {
        return order;
    }

    public static void main(String[] args) {
        // 使用邻接表表示图
        Graph graph = new AdjSet("g.txt");
        // 实例化一个 DFSGraph
        DFSGraph dfsGraph = new DFSGraph(graph);
        // 调用 dfs 方法进行深度优先遍历
        dfsGraph.dfs();
        // 打印出深度优先遍历的顺序
        System.out.println(dfsGraph.order());
    }
}

其中 g.txt 的内容如下

6 5
0 1
0 2
1 3
2 4
2 5

这个文件表示的图与我们在上面的动图中看到的图是一样的，我们来看下打印的结果

[0, 1, 3, 2, 4, 5]

这与我们在动图中看到的遍历顺序是一致的。

但是上面我们实现的深度优先遍历有一个小 bug，那就是上面的深度优先遍历只适合只有一个联通分量的图，如果有多个联通分量，那么其他联通分量中的节点就永远不可能被访问到，如

既然图中有节点永远不会被访问到，那么还能叫图的遍历吗，图的遍历可是要求能够访问图中所有的节点的，所以我们对代码进行改进

这次我们不只是从节点 $0$ 开始遍历，在遍历完节点 $0$ 所在的联通分量以后，我们检查是否还有节点没有遍历，即是否存在别的联通分量，如果有，那么我们还有遍历该节点所在的联通分量。

在最后我们进行一个扩展，我们知道树的深度优先遍历分为三种

• 前序遍历
• 中序遍历
• 后序遍历

图没有中序遍历，它分为两种

• 深度优先前序遍历
• 深度优先后序遍历

刚刚我们所编程的只是图的深度优先前序遍历，现在我们不妨写一下后序遍历的代码。在写代码之前，我们先明确后序遍历的这个后指的是什么，这个后在树的遍历中指的是先访问当前节点的孩子节点，然后访问当前节点，也就是访问当前节点在访问当前节点的孩子节点之后。类比于图，这个后指的就是先访问当前节点的邻接节点，然后再访问当前节

上面后序遍历的顺序为 $[3, 1, 4, 5, 2, 0]$，我们重构一下上面的代码，我们使用 preorder 来保存前序遍历的结果，使用 postorder 来保存后序遍历的结果：

import java.util.ArrayList;
import java.util.Arrays;

public class DFSGraph {
    private Graph graph;
    private ArrayList<Integer> preorder;
    private ArrayList<Integer> postorder;
    private boolean[] visited;

    public DFSGraph(Graph graph) {
        this.graph = graph;
        preorder = new ArrayList<>(graph.V());
        postorder = new ArrayList<>(graph.V());
        visited = new boolean[graph.V()];
        Arrays.fill(visited, false);
    }

    public void dfs() {
        for (int i = 0; i < visited.length; i++) {
            if (!visited[i]) {
                dfs(i);
            }
        }
    }

    private void dfs(int v) {
        visited[v] = true;
        // 前序遍历：在遍历相邻节点前，遍历当前节点
        preorder.add(v);
        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                dfs(w);
            }
        }
        // 后序遍历：遍历相邻节点后，再遍历当前节点
        postorder.add(v);
    }

    public Iterable<Integer> preorder() {
        return preorder;
    }

    public Iterable<Integer> postorder() {
        return postorder;
    }

    public static void main(String[] args) {
        Graph graph = new AdjSet("g.txt");
        DFSGraph dfsGraph = new DFSGraph(graph);
        dfsGraph.dfs();
        System.out.println(dfsGraph.postorder());
    }
}

打印的结果为

[3, 1, 4, 5, 2, 0]

深度优先遍历的应用

联通分量

第一个问题是如何求解图中有多少个联通分量。其实这个问题非常的简单，在上面的我们修改 DFS 的小 bug 时就提到，因为有多个联通分量，我们无法遍历完所有图中的节点，所以我们修改了代码

每次当我们在 for 循环中调用一次 dfs 的时候，就说明存在一个联通分量(Connected Component)，所以我们只要在调用 dfs 时统计联通分量的个数就可以，我们使用一个成员变量 ccount 来保存联通分量的个数

import java.util.Arrays;

public class CCGraph {
    private int cccount;
    private Graph graph;
    private boolean[] visited;

    public CCGraph(Graph graph) {
        this.graph = graph;
        this.cccount = 0;
        visited = new boolean[graph.V()];
        Arrays.fill(visited, false);
    }

    public void dfs() {
        for (int i = 0; i < visited.length; i++) {
            if (!visited[i]) {
                // 联通分量个数增加
                cccount++;
                dfs(i);
            }
        }
    }

    private void dfs(int v) {
        visited[v] = true;
        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                dfs(w);
            }
        }
    }

    public int getCccount() {
        return cccount;
    }

    public static void main(String[] args) {
        Graph graph = new AdjSet("g.txt");
        CCGraph ccGraph = new CCGraph(graph);
        ccGraph.dfs();
        int cccount = ccGraph.getCccount();
        System.out.println(cccount); // 2
    }
}

上面的代码与 DFSGraph 类的代码几乎是一致的，只不过统计了联通分量的个数。g.txt 中的内容为：

7 6
0 1
0 2
1 3
2 5
2 4
4 5

对于的图的形状如下：

可见上面的图有两个联通分量。

第二个与联通分量有关的问题是，我们希望得到每个联通分量中有多少个节点，以及分别包含哪些节点，我们可以使用一个 ArrayList 数组保存每个联通分量包含的节点，修改 dfs 如下

import java.util.ArrayList;
import java.util.Arrays;

@SuppressWarnings("all")
public class CCGraph {
    private int cccount;
    private Graph graph;
    private boolean[] visited;
    // 为什么不使用数组? 因为数组需要事先开辟空间，而我们事先不知道有多少个联通分量
    private ArrayList<ArrayList<Integer>> lists;

    // 构造函数对成员变量进行初始化
    public CCGraph(Graph graph) {
        this.graph = graph;
        this.cccount = 0;
        visited = new boolean[graph.V()];
        Arrays.fill(visited, false);
        lists = new ArrayList<>();
    }

    public void dfs() {
        for (int i = 0; i < visited.length; i++) {
            if (!visited[i]) {
                cccount++;
                // 每增加一个联通分量，新建一个 list 来保存该联通分量中包含的节点
                ArrayList<Integer> list = new ArrayList<>();
                lists.add(list);
                dfs(i, list);
            }
        }
    }

    private void dfs(int v, ArrayList<Integer> list) {
        visited[v] = true;
        // 将节点保存在所在联通分量对应的 list 中
        list.add(v);
        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                dfs(w, list);
            }
        }
    }

    public int getCCcount() {
        return cccount;
    }

    public ArrayList<ArrayList<Integer>> getCCList() {
        return lists;
    }
    
    // 判断两个节点是否在同一个联通分量中(是否连接)
    public boolean isConnected(int v, int w) {
        for (int i = 0; i < cccount; i++) {
            ArrayList list = lists.get(i);
            // 某联通分量中是否同时包含这两个节点
            if (list.contains(v) && list.contains(w)) {
                return true;
            }
        }
        // 所有的联通分量都不同时包含这两个节点，说明这两个节点不在同一个联通分量中
        return false;
    }

    public static void main(String[] args) {
        Graph graph = new AdjSet("g.txt");
        CCGraph ccGraph = new CCGraph(graph);
        ccGraph.dfs();
        int cccount = ccGraph.getCCcount();
        System.out.println(cccount); // 2

        // 打印出联通分量
        ArrayList<ArrayList<Integer>> lists = ccGraph.getCCList();
        for (int i = 0; i < cccount; i++) {
            // 获得每个联通分量对应的 list，里面保存了该联通分量包含的节点
            ArrayList<Integer> list = lists.get(i);
            // 打印出联通分量中包含的节点
            System.out.print(i + ": ");
            for (int v: list) {
                System.out.print(v + " ");
            }
            System.out.println();
        }
        
        System.out.println(ccGraph.isConnected(0, 5)); // true
        System.out.println(ccGraph.isConnected(0, 6)); // false
    }
}

上述的打印结果为

2
0: 0 1 3 2 4 5 
1: 6 
true
false

路径问题

所谓的路径问题就是求两个节点之间是否有路径，这个问题很简单，直接使用我们上面的 isConnected 方法就可以知道两个节点之间是否有路径了。不过我们更想知道的是，两个节点之间的路径是什么，即一个节点到达另一个节点会经历哪些节点。

对于下面的一幅图，我们想知道从节点 $0$ 到节点 $5$ 之间的路径

我们需要记录遍历时当前节点的前一个节点，例如遍历节点 $1$ 后会接着遍历节点 $3$，那么节点 $3$ 的前一个节点就是 $1$，通过这些信息就可以知道两个节点之间具体的路径。首先使用 DFS 图，在遍历的过程中记录信息，如下

在上面我们从节点 $0$ 开始遍历，在遍历的过程中我们记录了当前节点之前的节点，最后得到这么一个结果

现在我们想知道节点 $0$ 是如何到达节点 $5$ 的，直接逆推就可以知道路径为 $5 \leftarrow 4 \leftarrow 2 \leftarrow 0$，如下

这个算法可以求得节点 $0$ 与任何一个节点之间的路径，但是不能求得任意两点之间的路径，因为我们是从节点 $0$ 开始遍历的，如果我们想求得节点 $4$ 与节点 $5$ 之间的路径，那么我们需要从节点 $4$ 开始遍历，所以我们这种算法只能求解单源路径(Single Source Path) 问题。

在编程实现方面，我们使用一个 pre 数组来保存当前节点的前一个节点，例如，pre[3] = 1 就表示节点 $3$ 的前一个节点是节点 $1$

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;

public class SingleSourcePath {
    private Graph graph;
    private boolean[] visited;
    private int[] pre;
    // 从节点 s 开始遍历
    private int s;

    public SingleSourcePath(Graph graph, int s) {
        this.graph = graph;
        this.s = s;

        visited = new boolean[graph.V()];
        Arrays.fill(visited, false);

        pre = new int[graph.V()];
        Arrays.fill(pre, -1);

        // 默认认为源的前一个节点为自己，这个值访问不到，可以是任何值
        dfs(s, s);
    }

    private void dfs(int v, int parent) {
        visited[v] = true;
        pre[v] = parent;
        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                dfs(w, v);
            }
        }
    }

    public boolean isConnected(int t) {
        // 如果 pre[t] != -1，说明遍历到了该节点，则该节点与源节点是联通的
        return pre[t] != -1;
    }

    public Iterable<Integer> path(int t) {
        ArrayList<Integer> path = new ArrayList<>();
        // 如果不是联通的，直接返回
        if (!isConnected(t)) return path;

        int cur = t;
        while (cur != s) {
            path.add(cur);
            cur = pre[cur];
        }
        path.add(s);

        Collections.reverse(path);
        return path;
    }

    public static void main(String[] args) {
        Graph graph = new AdjSet("g.txt");
        SingleSourcePath singleSourcePath = new SingleSourcePath(graph, 0);
        System.out.println(singleSourcePath.path(5));
    }
}

其中 g.txt 为

7 6
0 1
0 2
1 3
2 5
2 4
4 5

对应的图就是上面的动图，输出为

[0, 2, 4, 5]

假设现在我们只想求源点 $s$ 到点 $t$ 之间的路径，而不是 $s$ 到任意一个点的路径，很明显我们的要求降低了，这意味着我们记录的信息更少，那我们算法可不可以加快呢?

当然可以，在上面我们求解源点 $s$ 到任意一点的路径，所以需要对源点 $s$ 所在的联通分量做 $DFS$，需要遍历联通分量中所有的节点，但是现在我们只需要求解到固定点 $t$ 的路径，我们不需要完整的做一遍 $DFS$，当我们遍历到节点 $t$ 时，就已经可以退出遍历了，提前终止遍历可以获得更快的性能。

假设我们需要求解源点 $0$ 到节点 $1$ 的路径

在编码上，在我们在设计 dfs 函数时，我们需要返回一个布尔值，代表是否已经找到节点 $t$，如果已经找到，我们就不需要做后续的遍历了，直接终止遍历

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;

public class Path {
    private Graph graph;
    private boolean[] visited;
    private int[] pre;

    private int s;
    private int t;

    public Path(Graph graph, int s, int t) {
        this.graph = graph;
        this.s = s;
        this.t = t;

        visited = new boolean[graph.V()];
        Arrays.fill(visited, false);

        pre = new int[graph.V()];
        Arrays.fill(pre, -1);

        dfs(s, s);
    }

    private boolean dfs(int v, int parent) {
        visited[v] = true;
        pre[v] = parent;
        // 如果已经找到，直接返回，不再继续遍历
        if (v == t) {
            return true;
        }
        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                // 如果在某相邻节点的深度优先遍历中找到节点 t，不再继续遍历其他相邻节点，提前返回
                if (dfs(w, v)) {
                    return true;
                }
            }
        }

        return false;
    }

    public boolean isConnected() {
        return visited[t];
    }

    public Iterable<Integer> path() {
        ArrayList<Integer> path = new ArrayList<>();
        if (!isConnected()) {
            return path;
        }

        int cur = t;
        while (cur != s) {
            path.add(cur);
            cur = pre[cur];
        }
        path.add(s);

        Collections.reverse(path);
        return path;
    }

    public static void main(String[] args) {
        Graph graph = new AdjSet("g.txt");
        Path path = new Path(graph, 0, 3);
        
        System.out.println(Arrays.toString(path.visited));
        System.out.println(path.path());
    }
}

输出为

[true, true, false, true, false, false, false]
[0, 1, 3]

从打印结果可以看出，我们并没有遍历所有的节点，这样提前终止遍历可以提高查找的速度。

无向图的环检测

我们怎么判断一幅图有没有环呢? 很简单，我们使用深度优先遍历，当访问到某节点时，如果该节点的某邻接节点已经被访问过，并且该邻接节点不是它的上一个节点，那么就说明该图中包含一个环

明白这一点以后我们就可以编写代码了

import java.util.Arrays;

public class CircleDetection {
    private Graph graph;
    private boolean[] visited;
    private boolean hasCircle;

    public CircleDetection(Graph graph) {
        this.graph = graph;
        visited = new boolean[graph.V()];
        Arrays.fill(visited, false);
        hasCircle = false;
    }

    public void dfs() {
        // 任一联通分量中有环，那么图中就有环
        for (int i = 0; i < visited.length; i++) {
            if (!visited[i]) {
                dfs(i, i);
            }
        }
    }

    private void dfs(int v, int parent) {
        visited[v] = true;
        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                dfs(w, v);
                // 进入下面的 if 判断就说明 w 已经访问过了
                // 如果 w 不是它的上一个节点，说明有环
            } else if (w != parent){
                hasCircle = true;
            }
        }
    }

    public boolean hasCircle() {
        return this.hasCircle;
    }

    public static void main(String[] args) {
        Graph graph = new AdjSet("g.txt");
        CircleDetection circleDetection = new CircleDetection(graph);
        circleDetection.dfs();
        System.out.println(circleDetection.hasCircle()); // true
    }
}

其中 g.txt 的内容如下

7 6
0 1
0 2
1 3
2 5
2 4
4 5

所对应的图如下

如果我们将节点 $2$ 和 $5$ 之间的边断开，那么图中是没有环的，新建 g2.txt 如下

7 5
0 1
0 2
1 3
2 4
4 5

Graph graph2 = new AdjSet("g2.txt");
CircleDetection circleDetection2 = new CircleDetection(graph2);
circleDetection2.dfs();
System.out.println(circleDetection2.hasCircle()); // false

另外，我们可以提前返回进行优化，如果我们已经找到了环，那么我们可以提前终止，后面就不需要继续查找了，我们修改 dfs 的返回值为 boolean 类型，这时 dfs 函数的含义就是从顶点 $v$ 开始，判断图中是否有环

public void dfs() {
    for (int i = 0; i < visited.length; i++) {
        if (!visited[i]) {
            if (dfs(i, i)) {
                hasCircle = true;
                // 不用查找其他联通分量了
                break;
            }
        }
    }
}

private boolean dfs(int v, int parent) {
    visited[v] = true;
    for (int w: graph.adj(v)) {
        if (!visited[w]) {
            if (dfs(w, v)) {
                // 如果已经在某相邻节点中找到环，不用再遍历其他的相邻节点
                return true;
            }
        } else if (w != parent){
            // 如果已经找到环，不用继续向后遍历
            return true;
        }
    }
    return false;
}

二分图检测

在这个小节我们来看一个二分图检测的问题，那么问题来了，什么叫二分图呢?

二分图需要满足一下两个特点：

1. 图中的节点被划分为两部分
2. 图中的边连接的是两个部分的节点

在上图中，节点 $0, 3, 4, 5$ 是一部分，节点 $1, 2, 6$ 是一部分，两部分的节点我使用不同的颜色进行填充；且图中所有的边都连接的是两个部分的节点。很明显上面的图满足二分图的两个特点，所以上面的图是一个二分图，那接下来的问题是如何检测一个图是否是一个二分图呢?

首先明白下面两个图是等价的

但是我们很难从右边的图中分辨出两部分的节点。

解决这个问题的关键是图中的所有边连接的是两个不同部分的节点，如果我们将对图进行深度优先遍历的过程中对节点染色，相同部分的节点染为一个颜色，因为所有的边都连接的是不同部分的节点，这意味着任意节点的邻接节点的颜色和自己都是不同的。

我们在遍历时将所有邻接节点的颜色染为和自己不一样，但是如果邻接节点已经染色，并且染的颜色和自己相同，与二分图的定义冲突，那么说明不是一个二分图，反之邻接节点染的颜色和自己不同，则继续遍历，如果遍历完整个图时都没有冲突，那么说明这个图就是一个二分图

代码如下：

import java.util.Arrays;

public class BinaryPartitionDetection {
    private Graph graph;
    private boolean[] visited;
    // 以 0 1 表示不同颜色
    private int[] colors;

    // 表示该图是否为二分图
    private boolean isBipartite;

    public BinaryPartitionDetection(Graph graph) {
        this.graph = graph;
        visited = new boolean[graph.V()];
        Arrays.fill(visited, false);
        // 初始化 colors 为 -1，表示未染色
        colors = new int[graph.V()];
        Arrays.fill(colors, -1);

        isBipartite = true;
    }

    public void dfs() {
        for (int i = 0; i < visited.length; i++) {
            if (!visited[i]) {
                // 如果在某联通分量中检测到不是二分图，不需要检测其他联通分量
                if (!dfs(i, 0)) {
                    isBipartite = false;
                    break;
                }
            }
        }
    }

    private boolean dfs(int v, int color) {
        visited[v] = true;
        // 染色
        colors[v] = color;
        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                // 0 => 1 - color = 1
                // 1 => 1 - color = 0
                // 如果已经在遍历某邻接节点的过程中检测到不是二分图，不需要遍历其他邻接节点
                if (!dfs(w, 1 - color)) {
                    return false;
                }
                // 进入 else if 表示该节点已经被访问过
                // 如果该节点的颜色与它的邻接节点相同，说明不是二分图，后面节点无需遍历
            } else if (colors[v] == colors[w]) {
                return false;
            }
        }
        return true;
    }

    public boolean isBipartite() {
        return isBipartite;
    }

    public static void main(String[] args) {
        Graph graph = new AdjSet("g3.txt");
        BinaryPartitionDetection binaryPartitionDetection = new BinaryPartitionDetection(graph);
        binaryPartitionDetection.dfs();
        System.out.println(binaryPartitionDetection.isBipartite()); // true
    }
}

其中 g3.txt 的内容如下

7 6
0 1
0 2
1 3
2 4
2 5
4 6

所表示的图如下，与动图中的图相同

在上面的实现中也使用了提前终止的技术，使用该技术可以很方便的提前终止遍历，提高程序的性能。

图的广度优先遍历

树的层序遍历

树的层序遍历是指一层一层的遍历树的节点，它的实现是借助于队列进行实现的：

每一次从队列的头部取出元素进行遍历，然后将该元素的左右孩子添加进队列，以此往复，直至队列为空，遍历结束。

import java.util.LinkedList;
import java.util.Queue;

public class BinaryTree {
    private class Node {
        private Node left;
        private Node right;
        private int value;
        
        public Node(int value) {
            this.value = value;
        }
    }
    
    private Node root;
    
    public BinaryTree(int value) {
        root = new Node(value);
    }
    
    public void levelOrder() {
        if (root == null) {
            return;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            Node node = queue.remove();
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
            System.out.println(node.value);
        }
    }
}

图的广度优先遍历

图的广度优先遍历与树的层序遍历相似，所谓的广度是指尽可能的遍历所有的相邻元素

广度优先遍历的实现同树的层序遍历类似，也是借助于队列这种数据结构，每次从队列的头部取出节点进行遍历，然后将该节点的所有相邻节点添加进队列，但是需要注意的是，因为图有可能发生重复遍历，所以需要使用visited 标记已遍历的节点；另外还需要考虑到有多个联通分量的情况，与深度优先遍历的写法类似

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;

public class BFSGraph {

    private Graph graph;
    private boolean[] visited;
    private ArrayList<Integer> order;

    public BFSGraph(Graph graph) {
        this.graph = graph;
        visited = new boolean[graph.V()];
        order = new ArrayList<>(graph.V());

        for (int i = 0; i < graph.V(); i++) {
            if (!visited[i]) {
                bfs(i);
            }
        }
    }

    private void bfs(int s) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(s);
        visited[s] = true;
        while (!queue.isEmpty()) {
            int v = queue.remove();
            order.add(v);
            for (int w: graph.adj(v)) {
                if (!visited[w]) {
                    queue.add(w);
                    visited[w] = true;
                }
            }
        }
    }

    public static void main(String[] args) {
        Graph graph = new AdjSet("g4.txt");
        BFSGraph bfsGraph = new BFSGraph(graph);
        System.out.println(bfsGraph.order);
    }
}

单源路径问题

对于路径问题的思路同DFS，使用一个 pre 数组，保存当前节点的上一个节点，当查询源节点到某个目的节点的路径时，只要从目的节点根据 pre 数组一直查找它的前一个节点，直到前一个节点为源节点就找到了路径

import java.util.*;

public class SingleSourcePath {
    private Graph graph;
    private int s;

    private boolean[] visited;
    private int[] pre;

    public SingleSourcePath(Graph graph, int s) {
        this.graph = graph;
        this.s = s;

        visited = new boolean[graph.V()];
        pre = new int[graph.V()];

        Arrays.fill(visited, false);
        Arrays.fill(pre, -1);

        bfs(s);
    }

    private void bfs(int s) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(s);
        visited[s] = true;
        pre[s] = s;

        while (!queue.isEmpty()) {
            int v = queue.remove();
            for (int w: graph.adj(v)) {
                if (!visited[w]) {
                    queue.add(w);
                    visited[w] = true;
                    pre[w] = v;
                }
            }
        }
    }

    private void validate(int v) {
        if (v < 0 || v >= graph.V()) {
            throw new IllegalArgumentException("v is out of index");
        }
    }

    public boolean isConnected(int t) {
        validate(t);
        return visited[t];
    }

    public ArrayList<Integer> path(int t) {
        ArrayList<Integer> res = new ArrayList<>();
        if (!isConnected(t)) {
            return res;
        }

        int cur = t;
        while (cur != s) {
            res.add(cur);
            cur = pre[cur];
        }
        res.add(s);

        Collections.reverse(res);
        return res;
    }

    public static void main(String[] args) {
        Graph graph = new AdjSet("g4.txt");
        SingleSourcePath singleSourcePath = new SingleSourcePath(graph, 0);
        // 0 -> 6: [0, 2, 6]
        System.out.println("0 -> 6: " + singleSourcePath.path(6));
    }
}

对于同样的图，使用深度优先遍历，结果是

0 -> 6: [0, 1, 3, 2, 6]

BFS 找到的路径比 DFS 找到的路径要短，这不是巧合，因为在无向无环图中，BFS 有一个重要的性质就是它寻找到的路径是最短路径，或者说经历的节点最少。为什么? 换种角度看，广度优先遍历是按照距离源的最小距离遍历的。

下面一个问题是寻找源到各点之间的距离，这个最简单的实现就是获得源到各点之间的路径，然后获得路径的长度即可推算出距离。下面提供一种更快的方法，无须先获得路径。首先我们需要声明一个 dis 数组来保存源到各点的距离，假设 w 是 v 的相邻节点，且 v 先被遍历，那么 s -> w 的距离为 s -> v + 1，即 dis[w] = dis[v] + 1

import java.util.*;

public class SingleSourcePath {
    private Graph graph;
    private int s;

    private boolean[] visited;
    private int[] pre;
    // dis 数组保存源到各节点的距离
    private int[] dis;

    public SingleSourcePath(Graph graph, int s) {
        this.graph = graph;
        this.s = s;

        visited = new boolean[graph.V()];
        pre = new int[graph.V()];
        // 初始化
        dis = new int[graph.V()];

        Arrays.fill(visited, false);
        Arrays.fill(pre, -1);
        // 初始化
        Arrays.fill(dis, -1);

        bfs(s);
    }

    private void bfs(int s) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(s);
        visited[s] = true;
        pre[s] = s;
        // 源到源的距离为 0
        dis[s] = 0;

        while (!queue.isEmpty()) {
            int v = queue.remove();
            for (int w: graph.adj(v)) {
                if (!visited[w]) {
                    queue.add(w);
                    visited[w] = true;
                    pre[w] = v;
                    // 更新 dis
                    dis[w] = dis[v] + 1;
                }
            }
        }
    }
    
    // 与 path 相关代码省略
    public int dis(int t) {
        validate(t);
        return dis[t];
    }
}

现实中有很多的问题可以建模为图论问题，然后使用 DFS 与 BFS 算法轻松的解决，现在我们打算从 LeetCode 选择几道题，来了解如何将现实问题建模为图论问题。

图论建模

二分图检测

题目介绍

给定一个无向图graph，当这个图为二分图时返回true。如果我们能将一个图的节点集合分割成两个独立的子集 A 和 B，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，我们就将这个图称为二分图。

graph 将会以邻接表方式给出，graph[i] 表示图中与节点 i 相连的所有节点。每个节点都是一个在 0 到graph.length-1 之间的整数。这图中没有自环和平行边： graph[i] 中不存在 i，并且 graph[i] 中没有重复的值。

注意:

• graph 的长度范围为 [1, 100]。
• graph[i] 中的元素的范围为 [0, graph.length - 1]。
• graph[i] 不会包含 i 或者有重复的值。
• 图是无向的: 如果 j 在 graph[i] 里边, 那么 i 也会在 graph[j] 里边。

解题思路

这道题的解法是对图中的节点染色，我们使用 DFS 遍历该图，如果当前节点的颜色为红色，那么就将它未访问过的相邻的节点染为绿色，如果当前节点颜色为绿色，就将未访问过的相邻节点染为红色，根据颜色来区分两个集合。

因为一条边连接的两个节点属于两个不同的几个集合，所以一条边连接的两个节点的颜色是不同的，如果我们在遍历的过程中发现已被访问过的相邻的节点的颜色与当前节点的颜色相同，说明它不符合二分图的定义，不是一个二分图；如果遍历图中所有的联通分量，都没有产生矛盾，说明这个图就是一个二分图。

class Solution {
    private boolean[] visited;
    // true 表示红色，false 表示绿色，默认为绿色
    private boolean[] colors;
    
    public boolean isBipartite(int[][] graph) {
        visited = new boolean[graph.length];
        colors = new boolean[graph.length];

        // 遍历所有的联通分量
        for (int i = 0; i < graph.length; i++) {
            if (!visited[i]) {
                if (!dfs(i, graph)) {
                    return false;
                }
            }
        }
        return true;
    }

    // dfs 返回一个布尔值，用以当不为二分图时提前终止遍历
    private boolean dfs(int v, int[][] graph) {
        visited[v] = true;

        for (int w: graph[v]) {
            // 如果未访问过，染为相反的颜色
            if (!visited[w]) {
                colors[w] = !colors[v];
                // 继续遍历
                if (!dfs(w, graph)) return false;
            // 如果已放访问过，且相邻节点颜色相同，不是二分图
            } else if (visited[w] && colors[w] == colors[v]) {
                return false;
            }
        }
        // 未发现矛盾，为二分图
        return true;
    }
}

岛屿的最大面积

题目介绍

给定一个包含了一些 0 和 1 的非空二维数组 grid 。一个岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0 (代表水) 包围着。

找到给定的二维数组中最大的岛屿面积(如果没有岛屿，则返回面积为 0 )。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

解题思路

我们将这个矩阵看做是一个图，矩阵中所有的 1 就是一个个的节点，如果两个 1 是垂直或者水平相邻的，那么就可以认为它们被一条边连着，即在一个联通分量中，而我们的任务就是找出包含节点最多的联通分量，并返回节点数目。

import java.util.Arrays;
import java.util.stream.Collectors;

public class Solution {
    private int rows;
    private int columns;
    private boolean[][] visited;
    private int[][] grid;

    public int maxAreaOfIsland(int[][] grid) {
        // 因为题目没说 grid 不为空，所以下面是对 grid 的一些校验
        if (grid == null) {
            return 0;
        }
        this.rows = grid.length;
        if (rows == 0) {
            return 0;
        }

        this.columns = grid[0].length;
        if (columns == 0) {
            return 0;
        }

        this.grid = grid;
        this.visited = new boolean[rows][columns];
        
        // 最大岛屿数目
        int max = 0;
        
        for (int row = 0; row < rows; row++) {
            for (int column = 0; column < columns; column++) {
                if (!visited[row][column] && grid[row][column] == 1) {
                    // dfs 返回的所在联通分量的节点数目
                    max = Math.max(max, dfs(row, column));
                }
            }
        }
        return max;
    }

    // 表示以 [row, column] 为起点进行 DFS 遍历所在联通分量包含的节点数目
    private int dfs(int row,int column) {
        int count = 1;
        visited[row][column] = true;

        for (int[] w: adj(row, column)) {
            int nextRow = w[0];
            int nextColumn = w[1];
            if (grid[nextRow][nextColumn] == 0) {
                continue;
            }
            if (!visited[nextRow][nextColumn]) {
                count += dfs(nextRow, nextColumn);
            }
        }
        return count;
    }

    // 获得当前节点四个方向上的相邻节点
    private Iterable<int[]> adj(int row, int column) {
        int[][] dirs = {{-1, 0}, {0, -1}, {0, 1}, {1, 0}};
        return Arrays.stream(dirs)
                .map(dir -> new int[]{dir[0] + row, dir[1] + column})
                .filter(item -> item[0] < rows && item[0] >= 0 && item[1] < columns && item[1] >= 0)
                .collect(Collectors.toList());
    }
}

二进制矩阵中的最短路径

题目介绍

在一个 $N \times N$ 的方形网格中，每个单元格有两种状态：空（0）或者阻塞（1）。现在我们的目标是从 $(0, 0)$ 到达 $(N-1, N-1)$，即从左上角到达右下角，而我们的目标是寻找一条最短路径，并且返回这条路径的长度。如果无法从左上角达到右下角，则返回 -1。

每个单元格有 8 种可能的方向

下面给出一个示例

解题思路

我们将方格看做是一个图，方格中所有的 0 看做是图一个节点，如果两个 0 在各自的 8 个方向之中，就说明这两个节点之间有一条边。为了求得最短路径，我们需要从左上角这个节点进行 BFS，使用 dis[i][j] 记录 $(i, j)$ 距离 $(0, 0)$ 的距离，所以 $dis[N-1][N-1]$ 也就表示从左上角到达右下角的最短路径。

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.stream.Collectors;

class Solution {
    private boolean[][] visited;
    private int[][] dis;
    private int rows;
    private int columns;

    public int shortestPathBinaryMatrix(int[][] grid) {
        this.rows = grid.length;
        this.columns = grid[0].length;

        if (grid[0][0] == 1 || grid[rows - 1][columns - 1] == 1) {
            return -1;
        }

        if (rows == 1 && grid[rows][columns] == 0) {
            return 1;
        }

        dis = new int[rows][columns];
        visited = new boolean[rows][columns];

        Queue<int[]> queue = new LinkedList<>();
        queue.add(new int[]{0, 0});
        visited[0][0] = true;
        dis[0][0] = 1;

        while (!queue.isEmpty()) {
            int[] location = queue.remove();
            int row = location[0];
            int column = location[1];

            for (int[] nextLocation: adj(row, column)) {
                int nextRow = nextLocation[0];
                int nextColumn = nextLocation[1];
                if (!visited[nextRow][nextColumn] && grid[nextRow][nextColumn] == 0) {
                    queue.add(new int[]{nextRow, nextColumn});
                    visited[nextRow][nextColumn] = true;
                    dis[nextRow][nextColumn] = dis[row][column] + 1;

                    if (nextRow == rows - 1 && nextColumn == columns - 1) {
                        return dis[nextRow][nextColumn];
                    }
                }
            }
        }

        return -1;
    }

    private Iterable<int[]> adj(int row, int column) {
        int[][] dirs = {{-1, 0}, {0, -1}, {0, 1}, {1, 0},
                {1, 1}, {-1, 1}, {1, -1}, {-1, -1}};
        return Arrays.stream(dirs)
                .map(dir -> new int[]{dir[0] + row, dir[1] + column})
                .filter(item -> item[0] < rows && item[0] >= 0 && item[1] < columns && item[1] >= 0)
                .collect(Collectors.toList());
    }
}

打开转盘锁

题目介绍

你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字： ‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’ 。每个拨轮可以自由旋转：例如把 ‘9’ 变为 ‘0’，’0’ 变为 ‘9’ 。每次旋转都只能旋转一个拨轮的一位数字。

锁的初始数字为 ‘0000’ ，一个代表四个拨轮的数字的字符串。列表 deadends 包含了一组死亡数字，一旦拨轮的数字和列表里的任何一个元素相同，这个锁将会被永久锁定，无法再被旋转。字符串 target 代表可以解锁的数字，你需要给出最小的旋转次数，如果无论如何不能解锁，返回 -1。

解题思路

我们把密码锁的一种组合称之为一种状态，例如 0000 这个组合表示的就是一种状态，现在我们的模板是将 0000 这种状态转变到 target 表示的状态，并且要求步骤最少。

我们可以把一种状态建模为图中的顶点，如果一个状态能够转变为另一种状态，我们就说这两个状态表示的节点之间存在一条边。对于密码锁来说，每一个拨轮可以前后滚动，共有四个拨轮，这意味着一个状态最多与 8 个状态相邻(考虑到 deadends，少于 8 个)，所以我们只要从 0000 这个状态开始 BFS 遍历，即可找到最少到 target 的拨动次数。

import java.util.*;
import java.util.stream.Collectors;

class Solution {
    public int openLock(String[] deadends, String target) {
        if ("0000".equals(target)) {
            return 0;
        }
        
        HashSet<String> deadSet = new HashSet<>();
        for (int i = 0; i < deadends.length; i++) {
            deadSet.add(deadends[i]);
        }

        if (deadSet.contains("0000")){
            return -1;
        }

        HashSet<String> visited = new HashSet<>();
        HashMap<String, Integer> dis = new HashMap<>();
        Queue<String> queue = new LinkedList();
        queue.add("0000");
        visited.add("0000");
        dis.put("0000", 0);

        while (!queue.isEmpty()) {
            String state = queue.remove();
            for (String nextState: adj(state, deadSet)) {
                if (!visited.contains(nextState)) {
                    queue.add(nextState);
                    visited.add(nextState);
                    dis.put(nextState, dis.get(state) + 1);

                    if (target.equals(nextState)) {
                        return dis.get(nextState);
                    }
                }
            }
        }

        return -1;
    }

    private Iterable<String> adj(String state, HashSet<String> deadSet) {
        ArrayList<String> list = new ArrayList<>();
        for (int i = 0; i < 4; i++) {
            char[] chars = state.toCharArray();
            char s = chars[i];
            chars[i] = Character.forDigit((chars[i] - '0' + 1) % 10, 10);
            list.add(new String(chars));
            chars[i] = s;
            chars[i] = Character.forDigit((chars[i] - '0' - 1 + 10) % 10, 10);
            list.add(new String(chars));
        }
        return list.stream().filter(s -> !deadSet.contains(s)).collect(Collectors.toList());
    }
}

倒水智力题

有两个桶，一个能装 5 升水，一个能装 3 升水，如何得到 4 升水?

这道题还是将状态看做是一个图的节点，如果状态之间能够互相转变，就说状态之前有一条边。我们定义状态 <x,y> 表示第一个桶有 x 升水，第二个桶有 y 升水。那么 <x, y> 与哪些状态是相连的呢，分为六种情况：

• 倒空第一桶水：<x, y> => <0, y>
• 倒空第二桶水：<x, y> => <x, 0>
• 加满第一桶水：<x, y> => <5, y>
• 加满第二桶水：<x, y> => <x, 3>
• 第二桶水倒入第一桶水：
  • $x + y \geq 5$：<x, y> => <5, x + y - 5>
  • $x + y < 5$：<x, y> => <x + y, 0>
• 第一桶水倒入第二桶水：
  • $x + y \geq 3$：<x, y> => <x + y - 3, 3>
  • $x + y < 3$：<x, y> => <0, x + y>

我们使用一个两位数表示一个状态，十位数表示第一个桶中有多少升水，个位数表示第二个桶中有多少升水，例如 23 表示第一个桶中有 2 升水，第二个桶中有 3 升水。

import java.util.*;

public class WaterPuzzle {
    public Iterable<Integer> waterPuzzle() {
        HashSet<Integer> visited = new HashSet<>();
        HashMap<Integer, Integer>  pre = new HashMap<>();
        Queue<Integer> queue = new LinkedList<>();

        queue.add(0);
        visited.add(0);
        pre.put(0, 0);
        
        // 保存最后找到的结果
        int endState = 0;
        // 用以跳出 while 循环
        boolean flag = false;
        
        while (!queue.isEmpty()) {
            int state = queue.remove();
            for (int nextState: adj(state)) {
                if (!visited.contains(nextState)) {
                    visited.add(nextState);
                    queue.add(nextState);
                    pre.put(nextState, state);
                    if (nextState / 10 == 4 || nextState % 10 == 4) {
                        endState = nextState;
                        flag = true;
                        break;
                    }
                }
            }
            if (flag) {
                break;
            }
        }


        ArrayList<Integer> result = new ArrayList();

        int cur = endState;
        result.add(cur);
        while (pre.get(cur) != 0) {
            cur = pre.get(cur);
            result.add(cur);
        }

        Collections.reverse(result);
        return result;
    }

    private Iterable<Integer> adj(int state) {
        int first = state / 10;
        int second = state % 10;

        Set<Integer> set = new HashSet<>();
        set.add(second);
        set.add(first*10);
        set.add(5*10 + second);
        set.add(first * 10 + 3);

        if (first + second >= 5) {
            set.add(5 * 10 + (first + second) - 5);
        } else {
            set.add((first + second) * 10);
        }

        if (first + second >= 3) {
            set.add((first + second - 3) * 10 + 3);
        } else {
            set.add(first + second);
        }

        return new ArrayList<>(set);
    }

    public static void main(String[] args) {
        WaterPuzzle waterPuzzle = new WaterPuzzle();
        for (int r: waterPuzzle.waterPuzzle()) {
            // 在个位数前加上0
            System.out.print((r >= 10 ? r : "0" + r) + " ");
        }
    }
}

输出为

50 23 20 02 52 43 

滑动谜题

题目介绍

在一个 2 x 3 的板上（board）有 5 块砖瓦，用数字 1~5 来表示, 以及一块空缺用 0 来表示。一次移动定义为选择 0 与一个相邻的数字（上下左右）进行交换。最终当板 board 的结果是 [[1,2,3],[4,5,0]] 谜板被解开。

给出一个谜板的初始状态，返回最少可以通过多少次移动解开谜板，如果不能解开谜板，则返回 -1 。

解题思路

我们将谜板上的一个组合看做是一个状态，一个状态就是图上的一个节点，如果一个状态能够转变到另一个状态，我们就说这两个状态节点之间有一条边连接。我们使用字符串来表示一个状态，例如 [[1, 4, 5], [0, 2, 3]] 这个状态表示为 "145023"，现在我们的目标是寻找一条从初始状态到 "123450" 这个状态的最短路径，使用 BFS 算法即可

import java.util.*;
import java.util.stream.Collectors;

public class Solution {
    private HashMap<String, Integer> visited = new HashMap<>();
    private int rows;
    private int columns;

    public int slidingPuzzle(int[][] board) {
        this.rows = board.length;
        this.columns = board[0].length;
        String initState = boardToString(board);

        if (initState.equals("123450")) {
            return 0;
        }
        Queue<String> queue = new LinkedList();
        queue.add(initState);
        visited.put(initState, 0);

        while (!queue.isEmpty()) {
            String state = queue.remove();
            for (String nextState: adj(state)) {
                if (!visited.containsKey(nextState)) {
                    queue.add(nextState);
                    visited.put(nextState, visited.get(state) + 1);

                    if ("123450".equals(nextState)) {
                        return visited.get(nextState);
                    }
                }
            }
        }

        return -1;
    }

    private String boardToString(int[][] board) {
        StringBuilder stringBuilder = new StringBuilder();
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                stringBuilder.append(board[i][j]);
            }
        }

        return stringBuilder.toString();
    }

    private Iterable<String> adj(String state) {
        ArrayList<String> result = new ArrayList<>();
        char[] chars = state.toCharArray();
        int index = state.indexOf("0");

        int row = index / columns;
        int column = index % columns;

        int[][] dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        List<Integer> locations = Arrays.stream(dirs)
                .map(dir -> new int[]{dir[0] + row, dir[1] + column})
                .filter(item -> item[0] < rows && item[0] >= 0 && item[1] < columns && item[1] >= 0)
                .map(item -> item[0] * columns + item[1])
                .collect(Collectors.toList());

        for (int i: locations) {
            String res = swap(chars, index, i);
            result.add(res);
            swap(chars, i, index);
        }

        return result;
    }

    private String swap(char[] chars, int i, int j) {
        char temp = chars[i];
        chars[i] = chars[j];
        chars[j] = temp;
        return new String(chars);
    }
}

桥和割点

桥

定义

我们首先看一下桥的概念

上面这幅图中，我们称节点 3-5 之间的这条边为桥，它具有什么特点呢? 一旦将这条边去掉，图的联通分量就会发生变化，所以有如下定义：

如果去掉某条边，使得图的联通分量发生变化，那么称这条边为桥。

桥可以看做是图中最脆弱的那条边，如果将交通系统建模为一个图的话，桥就是交通系统中最脆弱的部分，在军事中如果我们知道对方交通系统中的桥，那么我们就可以军事打击这个桥，使得对方的交通系统瘫痪。

寻找桥

如何判断某条边是不是桥，对于下图来说， 0-1 这条边是桥吗?

答案不是，因为去掉 0-1 这条边联通分量的个数没有增加，原因是节点 1 可以通过另一条路径 1->3->2->0 到达 0，所以我们判断某条边是不是桥，就是判断边的两个节点是否有另外一条路径。考虑边 v-w，如果存在另外一条路径，使得节点 v 可以到达节点 w 或者是节点 w 之前的节点，我们就认为 v-w 不是桥，否则没有另外的路径使得节点 v 到达节点 w，我们就认为 v-w 是桥。

为了完成这个判断，我们需要定义两个变量来帮助我们保存信息，一个是 order[] 数组，它保存的是以 DFS 遍历图的顺序，例如 order[0] = 0，表示节点 0 是第 0 个遍历的，order[3] = 2 表示节点 3 是第 2 个遍历的

另一个需要记录的信息是当前节点通过另外一条路径(即不是父节点那条路径)能够达到的顺序最前的节点，使用数组 low 表示，假设节点 2 能够达到最前的节点 0，而 order[0] = 0，所以 low[2] = order[0] = 0，初始 low[i] = order[i]，更新 low 数组有两个时机

• 节点 v 访问已被遍历过的邻接节点 w 时(该邻接节点不为父节点)，如果 low[w] < low[v]，则更新 low[v] = low[w]

  

  当我们访问到节点 2 时，接着访问节点 2 的邻接节点，访问到节点 0，节点 0 不是它的父亲节点(上一个节点)，而且节点 0 已经被访问过，并且 low[0] < low[2]，所以这个时候更新 low[2] = low[0]，表示节点 2 能通过另一条路径访问第 low[0] 个遍历的节点，即节点 2 能够访问到第 0 个被遍历的节点，即节点 0

• 访问完邻接节点 w，回到当前节点 v 时，如果邻接节点的 low[w] < low[v]，则更新 low[v] = low[w]

  

  当节点访问完节点 2 回到节点 3 时，此时 low[2] < low[3]，更新 low[3] = low[2] = 0，表示 low[3] 可以从另外一条路径到达第 low[2] = 0 个被遍历的节点，即节点 0

引入了 order 与 low 数组，接着我们可以根据这两个数组判断某条边是不是桥了，当我们遍历完相邻节点 w，来到当前节点 v 时，除了要更新 low[v]，我们还需要对这条边是不是桥进行判断。

我们需要判断 low[w] 与 order[v] 的大小，以此判断是否是桥。首先明确一下二者表示的意义：

• low[w] 表示节点 w 能够通过另一条路径能够到达的最前顺序，例如 low[w] = 3 就表示 w 节点能通过另一条路径到达第 3 个被遍历的节点，
• order [v] 表示节点 v 是第几个被遍历的

如果 low[w] $\leq$ order[v]，说明 w 能通过另一条路径到达节点 v 或 v 之前被遍历的节点，说明就不是桥，否则就是桥。

import java.util.ArrayList;
import java.util.HashSet;

public class FindEdge {
    private int[] order;
    private int[] low;
    private Graph graph;
    private boolean[] visited;
    private int count = 0;

    // 存储桥
    private ArrayList<int[]> result;

    public FindEdge(Graph graph) {
        this.graph = graph;
        order = new int[graph.V()];
        low = new int[graph.V()];
        result = new ArrayList<>();
        visited = new boolean[graph.V()];

        for (int i = 0; i < graph.V(); i++) {
            if (!visited[i]) {
                dfs(i, i);
            }
        }
    }

    private void dfs(int v, int parent) {
        visited[v] = true;
        low[v] = count;
        order[v] = count;
        count++;

        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                dfs(w, v);
                // 更新 low[v] 时机 1
                low[v] = Math.min(low[v], low[w]);
                // 判断是否是桥
                if (low[w] > order[v]) {
                    result.add(new int[]{v, w});
                }
            } else if (w != parent){
                // 更细 low[v] 时机 2
                low[v] = Math.min(low[w], low[v]);
            }
        }
    }

    public ArrayList<int[]> getResult() {
        return result;
    }
}

割点

定义

割点的定义与桥的定义类似，割点指的是一个节点，如果一旦移除这个节点，会导致图中的联通分量发生变化，那么就称这个节点为割点。

上图中节点 3 与节点 5 为割点，一旦去掉这两个节点之一，图的联通分量的个数就会发生变化。

寻找割点

寻找割点的过程同寻找桥是一样的，也需要维护 order 与 low 两个数组，这两数组的含义也是同上一致的。low 数组的更新时机以及更新过程也是同上一致的。

现在的问题是我们在什么时候判断某节点是不是割点，以及条件是什么。我们在遍历完相邻节点 w，返回到当前节点 v 时，如果 low[w] $\geq$ order[v] 时，就说明它是一个割点。这里的判断条件与桥的判断不同，桥的判断条件是如果 low[w] > order[v] 时，就说明 v-w 这条边是桥，注意多了一个等于号。

low[w] $\geq$ order[v] 表示节点 w 与 节点 v 之前被遍历的节点产生连接只能通过节点 v

例如节点 4 通过另外一条路径它最多到达节点 5，无法与节点 5 之前被遍历的节点产生连接。一旦节点 5 被删除，4 就无法访问到节点 0, 1, 2, 3，所以 5 就是割点。

但是添加了等于号之后，这个时候因为任何节点 low[v] $\geq$ order[0]，所以根节点 0 会被认为是割点，但根节点不一定是割点，这个时候我们就需要对根节点分别讨论，判断根节点是不是割点很简单，如果通过 DFS 遍历，根节点有两个相邻节点就说明它是割点

import java.util.ArrayList;
import java.util.HashSet;

public class FindCutPoints {
    private Graph graph;
    private boolean[] visited;
    private int[] order;
    private int[] low;
    private int count = 0;

    private HashSet<Integer> result = new HashSet<>();

    public FindCutPoints(Graph graph) {
        this.graph = graph;

        visited = new boolean[graph.V()];
        order = new int[graph.V()];
        low = new int[graph.V()];

        for (int i = 0; i < graph.V(); i++) {
            if (!visited[i]) {
                dfs(i, i);
            }
        }
    }

    private void dfs(int v, int parent) {
        visited[v] = true;
        order[v] = count;
        low[v] = count;
        count++;

        int child = 0;
        for (int w: graph.adj(v)) {
            child++;
            if (!visited[w]) {
                dfs(w, v);
                low[v] = Math.min(low[v], low[w]);
                if (v != parent && low[w] >= order[v]) {
                    result.add(v);
                }
                if (v == parent && child > 1) {
                    result.add(v);
                }
            } else if (w != parent) {
                low[v] = Math.min(low[v], low[w]);
            }
        }
    }

    public HashSet<Integer> getResult() {
        return result;
    }
}

哈密尔顿回路与哈密尔顿路径

哈密尔顿回路

1859年，爱尔兰数学家哈密尔顿（Hamilton）提出下列周游世界的游戏：在正十二面体的二十个顶点上依次标记伦敦、巴黎、莫斯科等世界著名大城市，正十二面体的棱表示连接这些城市的路线。试问能否在图中做一次旅行，从顶点到顶点，沿着边行走，经过每个城市恰好一次之后再回到出发点。

将上面的问题抽象为一个图论问题：如果我们能从图的某点出发，经过所有的节点有且仅有一次，并且回到原点，那么我们就说图中存在哈密尔顿回路。

哈密尔顿回路在数学上并没有找到充分必要条件，所谓充分必要条件指的是，如果图满足什么性质它就有哈密尔顿回路以及一旦图有哈密尔顿回路这个图就满足什么性质。所以我们判断判断某个图是否是哈密尔顿图，办法就是暴力搜索，使用回溯法去搜索图。

import java.util.ArrayList;
import java.util.Collections;

public class HamiltonCycle {
    private Graph graph;
    private boolean[] visited;
    // 还有多少个节点未访问，当 left == 0 时表示所有节点都被访问过
    private int left;
    // 当前节点的前一个节点，已获得路径
    private int[] pre;
    // 最后一个被访问的节点
    private int end;

    public HamiltonCycle(Graph graph) {
        this.graph = graph;
        this.visited = new boolean[graph.V()];
        this.left = graph.V();
        this.pre = new int[graph.V()];
        this.end = -1;

        pre[0] = 0;
        dfs(0);
    }

    // dfs 设有返回值，当找到哈密尔顿回路时，提前终止
    private boolean dfs(int v) {
        visited[v] = true;

        left--;

        if (left == 0 && graph.hasEdge(v, 0)) {
            end = v;
            return true;
        }

        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                pre[w] = v;
                if (dfs(w)) return true;
            }
        }
        visited[v] = false;
        left++;
        return false;
    }

    public Iterable<Integer> result() {
        ArrayList result = new ArrayList();

        if (end == -1) {
            return result;
        }

        int cur = end;
        while (cur != 0) {
            result.add(cur);
            cur = pre[cur];
        }
        result.add(0);

        Collections.reverse(result);
        return result;
    }
}

状态压缩

对图进行暴力搜索的时间复杂度是 $O(n!)$，所以暴力搜索图只适合图的规模不大的情况，当图的规模不大时，我们可以对 visited 数组进行压缩，使用一个整数来表示图中个节点的访问状态，具体就是根据这个数字的二进制位为 0 还是为 1 来表示是否被访问过。

举个例子，我们使用 int 类型来保存 visited 变量，int 类型占据 4 个字节，即 32 位，第一位是符号位，故可以认为可以表示 31 个节点访问状态，如果 visited = 1，二进制就是 00000000 00000000 00000000 00000001，从右往左数第 0 个数是 1，就表示节点 0 被访问过了，其他数字都是 0，表示其他节点没有被访问过。

观察上面的程序，我们对 visited 有三种操作：

• 判断某个节点有没有被访问过，例如判断节点 i 有没有被访问过，只要 $2^i$ 和 visited 相与即可知道，如果结果为 1，说明第 i 位为 1，即节点 i 被访问过，否则就是未被访问过
• 将节点 i 设置为被访问过(visited[i] = true)，也就是将第 i 个位置由 0 变为 1，就是将 $2^i$ 与 visited 异或即可
• 将节点 i 设置为未被访问过(visited[i] = false)，也就是将第 i 个位置由 1 变为 0，还是将 $2^i$ 与 visited 异或即可

注意 $2^i$ 可以表示为 i << 1

所以我们修改上面的程序，将 visited 数组变为一个数字

public class HamiltonCircleCompress {
    private Graph graph;
    private int visited;
    private int left;
    private int[] pre;
    private int end;

    // 不变
    public HamiltonCircleCompress(Graph graph) {
        this.graph = graph;
        this.visited = 0;
        this.left = graph.V();
        this.pre = new int[graph.V()];
        this.end = -1;

        pre[0] = 0;
        dfs(0);
    }

    private boolean dfs(int v) {
        // 设置 visited[v] 为 true
        visited = visited ^ (1 << v);
        left--;

        if (left == 0 && graph.hasEdge(v, 0)) {
            end = v;
            return true;
        }

        for (int w: graph.adj(v)) {
            // 判断 visited[w] 是否访问过
            if ((visited & (1 << w)) == 0) {
                pre[w] = v;
                if (dfs(w)) return true;
            }
        }
        
        // 设置 visited[v] 为 false
        visited = visited ^ (1 << v);
        left++;
        return false;
    }

    // 不变
    public Iterable<Integer> result() {
        ArrayList result = new ArrayList();

        if (end == -1) {
            return result;
        }

        int cur = end;
        while (cur != 0) {
            result.add(cur);
            cur = pre[cur];
        }
        result.add(0);

        Collections.reverse(result);
        return result;
    }
}

哈密尔顿路径

哈密尔顿路径的定义同哈密尔顿回路相似，如果从图中的某一点出发，能够经过图中所有的节点有且仅有一次，那么这条路径就是哈密尔顿路径。需要注意的是，图中是否存在哈密尔顿回路与起始点无关，但是哈密尔顿路径与起始点有关，可能从某点出发，并不能走过每一节点，但是从另一个节点出发，却能够走过所有节点，且只经过一次。

哈密尔顿路径的代码同哈密尔顿回路的代码相似，只有两处不同：

• 需要传入起始点
• 当 left 为 0 时，不用判断最后节点是否与起始点相邻，因为哈密尔顿路径不要求回到起始点

代码如下

import java.util.ArrayList;
import java.util.Collections;

public class HamiltonPath {
    private Graph graph;
    private boolean[] visited;
    private int left;
    private int[] pre;
    private int end;
    // 起始点
    private int s;

    public HamiltonPath(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        this.visited = new boolean[graph.V()];
        this.left = graph.V();
        this.pre = new int[graph.V()];
        this.end = -1;

        pre[0] = 0;
        dfs(s);
    }

    private boolean dfs(int v) {
        visited[v] = true;
        left--;

        // 不用判断 v 是否与起始点相邻
        if (left == 0) {
            end = v;
            return true;
        }

        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                pre[w] = v;
                if (dfs(w)) return true;
            }
        }
        visited[v] = false;
        left++;
        return false;
    }

    public Iterable<Integer> result() {
        ArrayList result = new ArrayList();

        if (end == -1) {
            return result;
        }

        int cur = end;
        while (cur != 0) {
            result.add(cur);
            cur = pre[cur];
        }
        result.add(0);

        Collections.reverse(result);
        return result;
    }
}

不同路径 III

这是一道 LeetCode 上的题目，它的本质就是在求哈密尔顿路径。

题目简介

在二维网格 grid 上，有 4 种类型的方格：

• 1 表示起始方格。且只有一个起始方格

• 2 表示结束方格，且只有一个结束方格

• 0 表示我们可以走过的空方格

• -1 表示我们无法跨越的障碍

返回在四个方向（上、下、左、右）上行走时，从起始方格到结束方格的不同路径的数目。每一个无障碍方格都要通过一次，但是一条路径中不能重复通过同一个方格。

**提示：1 <= grid.length * grid[0].length <= 20**。

解题思路

我们可以将整个二维网格建模为一幅图，0 表示一个节点(起始点 1 和终止点 2 也是节点)，如果两个 0 上下左右相邻，就表示它们之间有一条边。现在题目要求从起始点到达终止点，必须经过每一个节点，并且有且只能经过一次，这不就是哈密尔顿路径吗? 那么题目就是在要求这个图有多少条哈密尔顿路径。

import java.util.Arrays;
import java.util.stream.Collectors;

public class Solution {
    // 状态压缩，题目给出节点数目小于等于 20
    private int visited;
    // 起始点和终止点下标
    private int[] start;
    private int[] end;
    // 网格的行数和列数
    private int rows;
    private int columns;
    // 剩余未访问节点
    private int left;
    // 网格
    private int[][] grid;

    public int uniquePathsIII(int[][] grid) {
        this.grid = grid;
        this.rows = grid.length;
        this.columns = grid[0].length;
        this.visited = 0;
        this.start = new int[2];
        this.end = new int[2];
        this.left = rows * columns;

        // 下面这个循环是为了找到起始点和终止点，并且更新 left
        for (int row = 0; row < rows; row++) {
            for (int column = 0; column < columns; column++) {
                if (grid[row][column] == 1) {
                    start[0] = row;
                    start[1] = column;
                    grid[row][column] = 0;
                } else if (grid[row][column] == 2) {
                    end[0] = row;
                    end[1] = column;
                    grid[row][column] = 0;
                } else if (grid[row][column] == -1) {
                    // -1 不是节点，需要减掉
                    left--;
                }
            }
        }

        return dfs(start);
    }

    private int dfs(int[] v) {
        visited = visited ^ (1 << (v[0] * columns + v[1]));
        left--;
        if (left == 0 && (v[0] == end[0] && v[1] == end[1])) {
            visited = visited ^ (1 << (v[0] * columns + v[1]));
            left++;
            return 1;
        }

        int res = 0;
        for (int[] w: adj(v[0], v[1])) {
            if ((visited & (1 << (w[0] * columns + w[1]))) == 0 && grid[w[0]][w[1]] != -1) {
                res += dfs(w);
            }
        }

        // 回溯
        left++;
        visited = visited ^ (1 << (v[0] * columns + v[1]));
        return res;
    }

    private Iterable<int[]> adj(int row, int column) {
        int[][] dirs = {{-1, 0}, {0, -1}, {0, 1}, {1, 0}};
        return Arrays.stream(dirs)
                .map(dir -> new int[]{dir[0] + row, dir[1] + column})
                .filter(item -> item[0] < rows && item[0] >= 0 && item[1] < columns && item[1] >= 0)
                .collect(Collectors.toList());
    }

    public static void main(String[] args) {
        int[][] grid = {{1,0,0,0},{0,0,0,0},{0,0,2,-1}};
        Solution solution = new Solution();
        int res = solution.uniquePathsIII(grid);
        System.out.println(res);
    }
}

记忆化搜索

考虑这么一幅图

我们将它分为两部分

我们称左边为第一部分，右边为第二部分。现在从节点 0 开始遍历，寻找有多少条哈密尔顿回路，我们发现不论是以何种方式遍历完第一部分来到第二部分，有多少条哈密尔顿路径只与第二部分有关，即这几种路径搜索多少条哈密尔顿路径的结果是一样的，无需重复遍历。

例如，我们以 $0 \rightarrow 1 \rightarrow 2 \rightarrow 3$ 的方式遍历完第一部分来到第二部分

它有多少条哈密尔顿路径只与第二部分有关，如果我们以 $0 \rightarrow 2 \rightarrow 1 \rightarrow 3$ 的方式遍历完第一部分来到第二部分

它有多少条哈密尔顿路径的结果应该与以 $0 \rightarrow 1 \rightarrow 2 \rightarrow 3$ 顺序遍历的结果相同，如果我们可以缓存这个结果，就可以避免不必要的遍历，从而提高性能。

当遍历到节点 v 时，如果此时它们的 visited 是一样的，我们就可以认为它们会有一样的结果，例如对于上图，当遍历到节点 3 时，两条路径的遍历 visited 状态是一样的，我们可以认为它们的结果是一样的。

这种搜索策略叫做记忆化搜索，基于记忆化搜索的想法，我们改造上面的程序

import java.util.Arrays;
import java.util.HashMap;
import java.util.stream.Collectors;

public class Solution {
    private int visited;
    private int[] start;
    private int[] end;
    private int rows;
    private int columns;
    private int left;
    private int[][] grid;
    private HashMap<String, Integer> memo= new HashMap<>();

    public int uniquePathsIII(int[][] grid) {
        this.grid = grid;
        this.rows = grid.length;
        this.columns = grid[0].length;
        this.visited = 0;
        this.start = new int[2];
        this.end = new int[2];
        this.left = rows * columns;

        for (int row = 0; row < rows; row++) {
            for (int column = 0; column < columns; column++) {
                if (grid[row][column] == 1) {
                    start[0] = row;
                    start[1] = column;
                    grid[row][column] = 0;
                } else if (grid[row][column] == 2) {
                    end[0] = row;
                    end[1] = column;
                    grid[row][column] = 0;
                } else if (grid[row][column] == -1) {
                    left--;
                }
            }
        }

        return dfs(start);
    }

    private int dfs(int[] v) {
        String strV = format(v);

        if (memo.containsKey(visited + strV)) {
            return memo.get(visited + strV);
        }

        visited = visited ^ (1 << (v[0] * columns + v[1]));
        left--;
        if (left == 0 && (v[0] == end[0] && v[1] == end[1])) {
            visited = visited ^ (1 << (v[0] * columns + v[1]));
            left++;
            memo.put(visited + strV, 1);
            return 1;
        }

        int res = 0;
        for (int[] w: adj(v[0], v[1])) {
            if ((visited & (1 << (w[0] * columns + w[1]))) == 0 && grid[w[0]][w[1]] != -1) {
                res += dfs(w);
            }
        }

        left++;
        visited = visited ^ (1 << (v[0] * columns + v[1]));
        memo.put(visited+strV, res);
        return res;
    }

    private Iterable<int[]> adj(int row, int column) {
        int[][] dirs = {{-1, 0}, {0, -1}, {0, 1}, {1, 0}};
        return Arrays.stream(dirs)
                .map(dir -> new int[]{dir[0] + row, dir[1] + column})
                .filter(item -> item[0] < rows && item[0] >= 0 && item[1] < columns && item[1] >= 0)
                .collect(Collectors.toList());
    }

    private String format(int[] v) {
        int location = v[0] * columns + v[1];
        int first = location / 10;
        int second = location % 10;
        return "" + first + second;
    }
}

欧拉回路与欧拉路径

欧拉回路

七桥问题

18世纪初普鲁士的哥尼斯堡，有一条河穿过，河上有两个小岛，有七座桥把两个岛与河岸联系起来，如下图(黄色线条代表桥，绿色区域代表小岛和河岸)

有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。

数学家欧拉将河岸与小岛建模为节点，而七座桥建模为边，所以七桥问题建模为上图最右边的图论问题，找到图中经过所有边一次且回到原点的回路，这种回路我们后来称为欧拉回路。

欧拉回路的数学性质

上述的七桥问题很长时间都没有解决，即人们没有找到一条回路，能够只经过每座桥一次，然后回到原点。所以欧拉就猜想是不是根本不存在这种回路，经过他的证明，上述七桥问题的确不存在欧拉回路。

欧拉证明十分的简单，因为要从起点出发回到原点，那么对于每个节点都要一进一出，而每次进出需要消耗两条边，所以每个节点必须具有偶数条边，它才能保证有进有出，才有可能回到原点。所以就得到了欧拉回路一个充分必要条件：

每个节点的度都是偶数 $\Leftrightarrow$ 图中存在欧拉回路

每个节点的度都是偶数是图中存在欧拉回路是充分必要条件，二者可以互推，所以我们只要判断图中每个节点的度是不是偶数即可得到图中是否有欧拉回路这个结论。

回到七桥问题，观察图中的每一个节点，发现它们的度都不是偶数，所以绝对不可能从某点出发，经过所以的边一次然后回到原点，至此欧拉完美的解决了七桥问题，图论领域也是从此开始发展。

下面是判断欧拉回路是否存在的代码：

public class EulerCycle {
    private Graph graph;

    public EulerCycle(Graph graph) {
        this.graph = graph;
    }

    public boolean hasEulerCycle() {

        // 如果图中不只一个联通分量的话，说明肯定没有欧拉回路
        CCGraph ccGraph = new CCGraph(graph);
        if (ccGraph.getCCcount() != 1) {
            return false;
        }

        for (int i = 0; i < graph.V(); i++) {
            if (graph.degree(i) % 2 != 0) {
                return false;
            }
        }
        return true;
    }
}

求解欧拉回路

上面我们只是判断图中欧拉回路是否存在，但是我们没有得到一个具体的欧拉回路，所以在本节中介绍三种方法得到欧拉回路。

回溯法

回溯法就是暴力搜索法，搜索从起点出发的所有路径，直到找到一条欧拉回路

Fleury 算法

考虑下图，当我们从节点 0 来到节点 2 时

对于回溯法，可以选择遍历节点 1，也可以选择遍历节点 3，而 Fleury 算法却会选择接下来遍历节点 3 而不是节点 1，因为边 2-1 它是一个桥，如果选择遍历节点 1，就不可能再次回到节点 2，即节点 2 右边的边 2-3 2-4 不可能被访问到，所以 Fleury 算法的策略就是在遍历边前判断这条边是不是桥，如果是桥的话，就不遍历这条边，选择其他的边。

Hierholzer 算法

上图每个节点的度都是偶数，所以该图一定有欧拉回路。Hierholzer 算法首先在图中随便找到一个环

这个环如果是欧拉回路，那就找到了；如果不是欧拉回路，例如上面找到环 $0 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 0$，它不是欧拉回路，中间缺失了一环，因为节点 2 还与别的节点相连，上述链中的 $2$ 应该变为 $2 \rightarrow … \rightarrow 2 $，所以我们需要回退到节点 2 开始寻找这个环。

比如我们继续找到了 $2 \rightarrow 4 \rightarrow 5 \rightarrow 2$ 这个环

但是因为 $5$ 还与别的节点相连，所以 $5$ 应该被扩展为 $5 \rightarrow … \rightarrow 5$，所以又需要回退到节点 5 开始寻找新的环

最终我们找到了环 $5 \rightarrow 6 \rightarrow 7 \rightarrow 8 \rightarrow 5$，将这个结果替换 $2 \rightarrow 4 \rightarrow 5 \rightarrow 2$ 其中的 $5$，得到 $2 \rightarrow 4 \rightarrow 5 \rightarrow 6 \rightarrow 7 \rightarrow 8 \rightarrow 5 \rightarrow 2$，最后将这个结果环替换 $0 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 0$ 其中的 $2$，结果变为 $0 \rightarrow 1 \rightarrow 2 \rightarrow 4 \rightarrow 5 \rightarrow 6 \rightarrow 7 \rightarrow 8 \rightarrow 5 \rightarrow 2 \rightarrow 3 \rightarrow 0$。

我们可以使用栈来模拟上面的回退动作，当我们遍历环时，将节点添加进栈 result中，当我们发现来到某个节点不能继续遍历并且还有边未被遍历时，我们便进行回退，从栈中弹出元素，直到栈顶节点还与其他节点相连，从该节点开始寻找新的环。我们会将从栈中弹出的节点添加到另一个栈 back 中，当我们遍历完所有的边时在将 back 这个栈中的节点依次弹入到 result 这个栈中

因为上面有删边的动作，所以我们在 Graph 接口添加了一个 removeEdge(int v, int w)，作用就是将 v-w 这条边删除，具体实现如下

@Override
public void removeEdge(int v, int w) {
    validateVertex(v);
    validateVertex(w);
    sets[v].remove(w);
    sets[w].remove(v);
}

Hierholzer 算法的实现如下

import java.util.ArrayList;
import java.util.Collections;
import java.util.Stack;

public class EulerCycle {
    private Graph graph;

    public EulerCycle(Graph graph) {
        this.graph = graph;
    }

    public boolean hasEulerCycle() {

        CCGraph ccGraph = new CCGraph(graph);
        if (ccGraph.getCCcount() != 1) {
            return false;
        }

        for (int i = 0; i < graph.V(); i++) {
            if (graph.degree(i) % 2 != 0) {
                return false;
            }
        }
        return true;
    }

    public Iterable<Integer> result() {
        ArrayList res = new ArrayList();
        if (!hasEulerCycle()) return res;

        // 剩余未被遍历的边数
        int left = graph.E();
        Stack<Integer> result = new Stack<>();
        Stack<Integer> back = new Stack<>();

        int curV = 0;
        result.push(curV);
        // 还有边未被遍历就继续遍历
        while (left != 0) {
            // 每次更新 curV 为栈顶节点
            curV = result.peek();
            // 如果栈顶元素有相邻节点，从此寻找新的环
            if (graph.degree(curV) != 0) {
                // 获得一个相邻节点
                int w = graph.adj(curV).iterator().next();
                result.push(w);
                graph.removeEdge(curV, w);
                left--;
            } else {
                // 没有相邻节点，进行回溯
                back.push(result.pop());
            }
        }

        // 将 back 栈中的数据依次弹出到 result
        while (!back.isEmpty()) {
            result.push(back.pop());
        }

        // 将栈中元素弹出到 list 中
        while (!result.isEmpty()) {
            res.add(result.pop());
        }

        Collections.reverse(res);
        return res;
    }
}

验证算法是否正确，新建 g11.txt，内容如下

9 11
0 1
0 3
1 2
2 3
2 4
2 5
4 5
5 6
5 8
6 7
7 8

所表示的图就是示例中的图

测试如下

public static void main(String[] args) {
    Graph graph = new AdjSet("g11.txt");
    EulerCycle eulerCycle = new EulerCycle(graph);
    for (int w: eulerCycle.result()) {
        System.out.print(w + " ");
    }
}

输出为

0 1 2 4 5 6 7 8 5 2 3 0 

与我们讨论的结果一致。

最小生成树

带权图

在之前的文章中，介绍的都是无向无权图，那本篇开始介绍无向带权图

如果将上述的图看做是一个交通系统的话，那么边的权重就可以代表为距离。为了表示带有权重的图，我们建立一个 WeightedGraph 类来表示带权图。

同无权图 AdjSet 一样，我们从如下格式的文件读取内容生成图

7 12
0 1 2
0 3 7
0 5 2
1 2 1
1 3 4
1 4 3
1 5 5
2 4 4
2 5 4
3 4 1
3 6 5
4 6 7

第一行 7 表示总共有 7 个节点，12 表示有 12 条件，下面表示两两相邻的节点，以及之间的权重，例如 0 1 2 表示节点 0 与节点 1 相邻，之间的权重为 2。

WeightedGraph 类如下，代码大部分同 AdjSet 类：

import java.io.File;
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;

public class WeightedGraph{
    private int V;
    private int E;
    // adj[i] 是一个 HashMap，键为相邻的节点，值为边上的权重
    private HashMap<Integer, Integer>[] adj;

    public WeightedGraph(String path) {
        File file = new File(path);
        Scanner scanner = null;

        // 从 txt 文件读取建立图，大部分同 AdjSet 类
        try {
            scanner = new Scanner(file);
            this.V = scanner.nextInt();
            if (V < 0) {
                throw new IllegalArgumentException("V can't be negative");
            }
            adj = new HashMap[V];
            for (int i = 0; i < V; i++) {
                adj[i] = new HashMap<>();
            }

            this.E = scanner.nextInt();
            if (E < 0) {
                throw new IllegalArgumentException("E can't be negative");
            }

            for (int i = 0; i < E; i++) {
                int v = scanner.nextInt();
                int w = scanner.nextInt();
                int weight = scanner.nextInt();

                if (v == w) {
                    throw new IllegalArgumentException("存在自环边");
                }
                if (adj[v].containsKey(w)) {
                    throw new IllegalArgumentException("存在平行边");
                }

                adj[v].put(w, weight);
                adj[w].put(v, weight);
            }
        } catch (Exception e) {
            e.printStackTrace();
        }finally {
            scanner.close();
        }
    }

    public int V() {
        return this.V;
    }

    public int E() {
        return this.E;
    }

    public int getWeight(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return adj[v].get(w);
    }

    public int degree(int v) {
        validateVertex(v);
        return adj[v].size();
    }

    public boolean hasEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return adj[v].containsKey(w);
    }

    public Iterable<Integer> adj(int v) {
        validateVertex(v);
        return adj[v].keySet();
    }

    public void validateVertex(int v) {
        if (v < 0 && v >= V) {
            throw new IllegalArgumentException("节点超过 [0, V) 的范围");
        }
    }

    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder();
        stringBuilder.append(String.format("V: %d, E: %d\n", this.V, this.E));
        for (int v = 0; v < this.V; v++) {
            stringBuilder.append(String.format("%d : ", v));
            for (Map.Entry w: adj[v].entrySet()) {
                stringBuilder.append(String.format("(%d: %d) ", w.getKey(), w.getValue()));
            }
            stringBuilder.append("\n");
        }
        return stringBuilder.toString();
    }
}

最小生成树

首先介绍生成树的概念，假设图中有 $V$ 个顶点，如果能找到图中 $V - 1$ 条边这 $V$ 个节点连接起来，那么就说这 V 个节点与 V - 1 条边形成的图叫做这个图的生成树。

例如图的 DFS 遍历以及 BFS 遍历就会形成一个生成树

只要图中的 $V - 1$ 条边将图中的 $V$ 个顶点联通起来，那么就是图的一个生成树，所以一个图有很多的生成树，所谓的最小生成树，就是生成树边上的权值加起来最小

那么最小生成树有什么应用呢? 如果将这个图看做是交通系统，找出最小生成树就是找到一种耗费最低的方式将所有站点连通起来的布局方案。

切分定理

下面介绍切分定理，这个定理被用来寻找最小生成树。首先什么叫切分，所谓切分就是把节点分为两部分

上图中节点 $0, 5, 4$ 被划分一部分，其余节点为另一部分。切分的方式有很多种，随意你进行切分，只要将图中的节点划分为两部分即可。

引入了切分的概念，下面继续引入横切边的概念。所谓的横切边指的是将两个不同部分节点连接起来的边，例如对于上面的划分，有如下横切边

上面被标记为绿色的边就是横切边，可以看到横切边的两端是两个不同部分的节点。

介绍完必须的概念之后，引入切分定理：

切分定理：对于任意一个切分，这种切分形成的横切边中，权值最小的横切边一定在最小生成树中

这个定理很好证明，我们根据切分将图分为两部分

这两部分之间的边就是横切边，可以观察到横切边将这两个部分连接在了一起，为了使得生成树连通，一定要在横切边中选择一条边，而为了得到最小生成树，那当然选择的是权值最小的横切边，所以说权值最小的横切边一定在最小生成树中。

Kruskal 算法

Kruskal 算法是求的最小生成树的一种算法，他的思想很简单，就是每次取图中最小的边，只要这条边没有已经选取的边形成环。例如对于下图

首先选择图中最短的两条边，即权值为 1 的两条边 1-2 与 3-4

下面继续选择权值最小的边，选择 0-5、0-1，这两条边的权值为 2

继续选择权值最小的边，此时选择 1-4，权值为 3

继续选择，此时应该选择 5-2 与 1-3 两条边，它们的权值为 4，但是我们发现选择 5-2 就会形成一个环，选择 1-3 也会形成环，所以这两条边不能选，生成树中可不能有环的。除开这两条边继续选择，发现 5-1、3-6 这两条边的权值为 5，权值最小，但是选择 5-1 就会形成环，所以不选 5-1，只选择 3-6

这个时候我们已经找到了 6 条边将这 7 个顶点连接起来，即找到了一个最小生成树

Kruskal 的算法思想很简单，就是贪心，每次选择权重最小的边，但是怎么证明这种贪心策略是对的。这就需要用到切分定理。

每次我们选择最小的边，我们只需要让这条边是一个切分的横切边就行，这种切分很好做，让这条边两个节点属于不同的部分即可，根据切分定理这条横切边一定是最小生成树中的一条边。如果这条边与选择的边形成了一个环，这说明找不到一个切分，使得这条边的所有横切边中最短的边，所以不能选择它。

在代码的实现方向，每次我们找到一个最短的边时，需要判断是否构成一个环，例如我们找到边 5-1，需要判断添加这条边是否构成一个环，其实就是在检测在添加这条边之前节点 5 和节点 1 是否连通，如果是连通，添加这条边后就会形成环。

每次都需要判断两个节点需要连通，可以使用 DFS 来做，但是这样做复杂度太高，借助并查集这种数据结构可以很方便的判断两个节点是否连通，只需要判断它们是否在一个集合中即可，如果对于并查集不熟，可以参考这篇文章。

并查集的实现如下：

public class UnionFind {
    private int[] parent;
    private int[] rank;

    public UnionFind(int size) {
        parent = new int[size];
        rank = new int[size];

        for (int i = 0; i < parent.length; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    public int getSize() {
        return parent.length;
    }

    private int find(int index) {
        if (index < 0 || index >= parent.length) {
            throw new IllegalArgumentException("参数错误");
        }

        while (index != parent[index]) {
            index = parent[index];
        }
        return index;
    }

    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    public void unionElements(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) {
            return;
        }

        if (rank[pRoot] <= rank[qRoot]){
            parent[pRoot] = parent[qRoot];
            if (rank[pRoot] == rank[qRoot]) {
                rank[qRoot]++;
            }
        } else {
            parent[qRoot] = parent[pRoot];
        }
    }
}

我们需要一个类来保存边的信息，这里我们新建一个 WeightedEdge 类：

public class WeightedEdge {
    private int v;
    private int w;
    private int weight;

    public WeightedEdge(int v, int w, int weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public int getV() {
        return v;
    }

    public int getW() {
        return w;
    }

    public int getWeight() {
        return weight;
    }

    @Override
    public String toString() {
        return String.format("(%d-%d: %d)", v, w, weight);
    }
}

Kruskal 算法实现如下：

import java.util.ArrayList;
import java.util.Collections;

public class Kruskal {
    private WeightedGraph graph;
    public ArrayList<WeightedEdge> result = new ArrayList<>();

    public Kruskal(WeightedGraph graph) {
        this.graph = graph;
        int V = graph.V();

        // 将所有的边添加进集合中
        ArrayList<WeightedEdge> edges = new ArrayList<>();
        for (int v = 0; v < V; v++) {
            for (int w: graph.adj(v)) {
                if (v < w) {
                    edges.add(new WeightedEdge(v, w, graph.getWeight(v, w)));
                }
            }
        }
        
        
	    // 根据边的权值大小，从小到大排序
        Collections.sort(edges, (w1, w2) -> w1.getWeight() - w2.getWeight());
        UnionFind unionFind = new UnionFind(V);
        for (WeightedEdge edge: edges) {
            int v = edge.getV();
            int w = edge.getW();
            // 如果之前不连通
            if (!unionFind.isConnected(v, w)) {
                result.add(edge);
                unionFind.unionElements(v, w);
            }
        }
    }

    public Iterable<WeightedEdge> result() {
        return result;
    }
}

Prim 算法

Prim 算法也是有关最小生成树的算法，它的思想同切分定理密切相关。因为对于每一个切分，权值最小的横切边一定在最小生成树中。Prim 算法就在遍历节点的过程中，将遍历到的节点与未遍历的节点作为两部分形成一个切分，然后遍历此时所有的横切边，在此边作为最小生成树的一条边。

每次遍历到一个节点即可找到一条横切边，当遍历到最后一个节点时，就能找到 $V-1$ 条边，即可形成一个生成树，并且根据切分定理，这个生成树一定是最小生成树。

Prim 算法最后的结果是同 Kruskal 算法相同的。

在代码的实现方面，因为每次产生一次新的切分，都要找到所有的横切边进行遍历然后找到最小的横切边，这个过程我们可以使用优先队列进行实现。

当遍历到一个节点时，新的横切边的产生都与这个遍历到的节点相连，我们只要将新的横切边添加到队列中即可，不用遍历节点寻找所以的横切边，另外这是一个优先队列，即队首元素它的权重是最小的，我们也不用查找最小边的炒作，直接取出队首元素即可。

另外，可能你会注意到，当遍历到一个新的节点，产生一个新的切分时，之前的横切边可能不是横切边了，即优先队列中的边不是所有的边都是横切边。仔细想想，这个并没有影响，因为虽然不是所有的边都是横切边，但是所有的横切边都在队列里，我们从队列中取出边时进行判断，不是横切边直接忽略即可，完全不影响我寻找最小的横切边。

import java.util.ArrayList;
import java.util.PriorityQueue;

public class Prim {
    private WeightedGraph graph;
    private boolean[] visited;
    private ArrayList<WeightedEdge> result = new ArrayList<>();

    public Prim(WeightedGraph graph) {
        this.graph = graph;
        PriorityQueue<WeightedEdge> priorityQueue = 
            new PriorityQueue<>((w1, w2) -> w1.getWeight() - w2.getWeight());
        this.visited = new boolean[graph.V()];
        
        visited[0] = true;
        for (int w: graph.adj(0)) {
            priorityQueue.add(new WeightedEdge(0, w, graph.getWeight(0, w)));
        }

        while (!priorityQueue.isEmpty()) {
            WeightedEdge edge = priorityQueue.remove();
            int v = edge.getV();
            int w = edge.getW();
            // 不是横切边直接忽略
            if (visited[v] && visited[w]) {
                continue;
            }
            result.add(edge);
            visited[w] = true;
            // 添加新的横切边
            for (int next: graph.adj(w)) {
                priorityQueue.add(new WeightedEdge(w, next, graph.getWeight(w, next)));
            }
        }

    }

    public Iterable<WeightedEdge> result() {
        return result;
    }
}

如果在实际中需要手写最小生成树算法，推荐使用 Prim 算法，因为在大多数的语言标准库中都有优先队列的实现，但是都没有并查集的实现，所以如果使用 Kruskal 算法需要手写并查集。

最短路径算法

本文讲解图中点与点之间的最短路径问题，主要讲解三个算法：

• Dijkstra 算法
• Bellman-Ford 算法
• Floyed 算法

其中 Dijkstra 与 Bellman-Ford 是解决单源最短路径问题，即它只能求解某节点到其他节点的最短路径，而 Floyed 算法能够求解所有节点之间的最短路径。

Dijkstra 算法

Dijkstra 算法它能够求解单源最短路径问题，并且使用该算法有一个前提，图中不能存在负权边，即图中的每条边的权值都必须是大于等于 0 的。

Dijkstra 算法使用一个 dis 数组来表示从源 s 到其他节点的最短距离，例如 dis[v] 表示的就是源 s 到达节点 v 的最短距离，在初始时，除了 dis[s] 为 0，其余的 dis[v] 均为无穷大。

Dijkstra 算法的思想是，每次从未遍历的节点，寻找在 dis 数组中值最小的节点，然后根据这个节点更新其未被遍历过的相邻节点在 dis 数组中的值。例如遍历到节点 v，其相邻节点为 w，并且节点 w 未被遍历过，如果 dis[v] + weight(v,w) < dis[w]​，那么就更新 dis[w]，其中 weight(v, w) 是边 v-w 的权值。

举个例子，假设源为节点 0，我们求解节点 0 到各个节点的最短路径

初始节点 0 到节点 0 的距离为 0，其余节点距离节点 0 的距离为 $\infin$。根据 Dijkstra 算法，每次从未遍历的节点，寻找在 dis 数组中值最小的节点，所以此时我们找到了节点 0，dis[0] 为 0，比其他元素小。我们来到节点 0，根据公式 dis[0] + weight(0, w) < dis[w]更新与 0 相邻的节点 w

继续从未遍历的节点，寻找在 dis 数组中值最小的节点，是节点 2，它的值为 1，并且此时我们可以断定节点 0 离节点 2 的最短距离就是 1。

为什么呢? 假设存在一条更短的路径从 0 到 2，例如是 0-1-2，但是因为此时 0-2 是最小的，而图中又不存在负权边，所以 0-1-2 比 0-1 还大，也就是比 0-2 大，所以 0-2 就是从 0 到 2 的最短路径。来到节点 2 之后，根据条件 dis[2] + weight(2, w) < dis[w] 是否成立更新其相邻节点。

继续从未遍历的节点，寻找在 dis 数组中值最小的节点，此时 dis[1] 与 dis[6] 的值都是 2，随便选一个就可以，这里我选择节点 1，并且此时可以判定节点 0 到节点 1 的最短路径就是 dis[1] 为 2。为什么?

假设存在一条路径经过未遍历的节点从 0 到达节点 1，比如是节点 4 好了，因为 dis[1] 此时是未遍历的节点中最小的，所以 dis[1] < dis[4]，更别说还要加上节点 4 到节点 1 的距离，矛盾，所以找不到一条经过未遍历节点来到节点 1。

那么是否存在一条路径只经过已经遍历过的节点到达节点 1，并且路径比 dis[1] 小，不妨假设存在这么一条路径 0 -> ... -> s -> 1，它的值比 dis[1] 小，即 dis[s] + weight(s, 1) < dis[1]，那么当我们之前遍历到节点 s 对相邻节点更新的时候就会更新 dis[1] 为更小的值，也产生了矛盾，因此也不存在一条路径只经过已经遍历过的节点到达节点 1。所以我们可以说此时的 dis[1] 就是从 0 到 1 的最短路径。

来到节点 1 之后，更新其未被遍历过的相邻节点的值，当然图中节点 1 此时不存在未被遍历过的相邻节点，所以不进行任何的更新

继续从未遍历的节点，寻找在 dis 数组中值最小的节点，找到节点 6，此时 dis[6] 的值为 2，并且此时我们可以判定从节点 0 到节点 6 的最短距离就是 2。

分析方法同上，先假设存在一条从未被遍历过的节点到达节点 6 得到的更短路径，但是因为 dis[6] 已经是从 0 到未被遍历的节点最小的，图中又不存在负权边，所以矛盾，再做假设存在只经过已被遍历过的节点到达节点 6，那么在之前 dis[6] 的值就会被更新为更小的值，也会产生矛盾，从而得到结论，不存在另外一条路径从 0 到 6 更短，此时 dis[6] 就是从 0 到 6 的最短距离。

来到节点 6 之后根据条件更新其未被遍历的相邻节点，图中节点 6 不存在未被遍历过的相邻节点，因此不作更新

继续从未遍历的节点，寻找在 dis 数组中值最小的节点，发现 dis[3] 和 dis[4] 都是 3，我们就随便选择一个，这里选择节点 3，并且此时可以判定 dis[3] 是从节点 0 到节点 3 的最短距离，已经分析过多次，不再分析。

来到节点 3 之后，根据条件更新其未被遍历过的相邻节点，与节点 3 相邻未被遍历过的节点就是节点 4，但是并不满足 dis[3] + 3 < dis[4] 的条件，所以不更新 dis[4]

重复上面的过程，我们可以得到下面这张表

	0	1	2	3	4	5	6
dis	0	2	1	3	3	4	2

第二行的值表示原点到各点的最短路径。

所以 Dijkstra 算法就始终在重复两步：

• 寻找未被遍历节点中在 dis 数组中最小的那个节点
• 根据条件更新未被遍历过的相邻节点

寻找最小节点的操作我们使用一个优先队列来完成，直接从队首取出的值就是最小的，无需寻找

import java.util.*;

public class Dijkstra {
    private WeightedGraph graph;
    private int s;
    private int[] dis;
    private boolean[] visited;
    // 求具体的路径用
    private int[] pre;

    public Dijkstra(WeightedGraph graph, int s) {
        this.graph = graph;
        graph.validateVertex(s);
        this.s = s;

        this.dis = new int[graph.V()];
        this.visited = new boolean[graph.V()];
        this.pre = new int[graph.V()];

        // 初始化操作
        Arrays.fill(pre, -1);
        Arrays.fill(dis, Integer.MAX_VALUE);

        pre[s] = s;
        dis[s] = 0;

        // 建立一个优先队列，Node 保存的是节点 dis[v] 的值
        PriorityQueue<Node> queue =
                new PriorityQueue<>((node1, node2) -> node1.getDis() - node2.getDis());
        queue.add(new Node(s, 0));
        while (!queue.isEmpty()) {

            // 选出最小节点
            int v = queue.remove().getV();

            // 可能存在重复添加的情况，忽略
            if (visited[v]) {
                continue;
            }
            visited[v] = true;

            // 更新未被遍历的相邻节点
            for (int w: graph.adj(v)) {
                if (!visited[w]) {
                    dis[w] = Math.min(dis[w], dis[v] + graph.getWeight(v, w));
                    // 将 dis[w] 添加进队列，可能会重复添加
                    // 不过我们只对最小的那个感兴趣，重复添加取出后会被忽略
                    queue.add(new Node(w, dis[w]));
                    pre[w] = v;
                }
            }
        }
    }

    public int[] result() {
        return dis;
    }

    // 获得源到节点 t 的具体路径
    public Iterable<Integer> path(int t) {
        ArrayList<Integer> path = new ArrayList<>();
        if (!visited[t]) {
            return path;
        }
        int cur = t;
        while (cur != s) {
            path.add(cur);
            cur = pre[cur];
        }
        path.add(s);

        Collections.reverse(path);
        return path;
    }
}

Bellman-Ford 算法

Bellman-Ford 算法也是求解单源最短路径的算法，与 Dijkstra 算法不同的是，它能够处理负权边，即使允许图中存在权值为负数的边。

在讲解 Bellman-Ford 算法之前，我们来看一组操作

dis[w] = Math.min(dis[w], dis[v] + graph.getWeight(v, w));

这个操作叫做松弛操作。

为什么叫松弛，因为本来可以直接到达点 w，现在经过上面的操作之后，偏要经过点 v 然后到达 w (不一定会经过，只有当 dis[v] + graph.getWeight(v, w) < dis[w] 才会经过点 v)，如果把边看做橡皮筋的话，不就相当于松弛了吗?

而 Bellman-Ford 算法就是，对所有的边进行 $V - 1$ 轮松弛操作，这个 $V$ 指的是图中的节点数目，经过 $V - 1$ 轮松弛操作后，此时 dis 数组中保存的就是源点到各个节点的最短路径。

为了理解 Bellman-Ford 算法为什么这么神奇，每个节点经过 $V-1$ 轮松弛操作之后就可以得到最短路径，我们还是要研究一下松弛操作

dis[w] = Math.min(dis[w], dis[v] + graph.getWeight(v, w));

如果进行了松弛操作，意味源多经过了一条边到 w，所以如果我们设定 dis[w] 为源点最多经过 $k$ 条边到达点 w 的最短路径，那么经过一次松弛操作之后 dis[w] 语义变为源点最多经过 $k + 1$ 条边到达点 w 的最短路径，因为一个节点到达另一个节点最多经过 $V-1$ 条边，因此经过 $V - 1$ 轮的松弛操作之后，dis[w] 语义变为了源点最多经过 $V - 1$ 条边到达点 w 的最短路径，考虑到了源点到达节点 w 能经过的边数的所有情况，所以最终的 dis[w] 就是源点到点 w 的最短路径。

我们来看一个例子，假设源点为 0

图中有 4 个节点，因此要进行 3 轮松弛操作。第一次对所有边进行松弛操作

第二次对所有边进行松弛操作

第三次对所有边进行松弛操作

最后得到的结果为

	0	1	2	3
dis	0	4	1	2

Bellman-Ford 虽然能够处理负权边，但是如果图中有负权环的话，那么就无法求解了，所谓的负权环是指环中所以边的路径和为负值，这样的只要我每次经过一次环，每个节点的 dis 值都在减少，如果图中存在负权环的话，那么根本就不存在最小路径。

大家在考虑一个问题，对于无向图来说，如果图中出现了负权边意味着什么? 假设 0-1 是一个负权边，因为是无向图，可以从 0 到 1，也可以从 1-0，那么我们可以从 0 来到 1，然后从 1 来到 0，这就形成一个负权环。所以 Bellman-Ford 算法其实是一个有向图算法。

另外我们可以通 Bellman-Ford 算法检测图中是否存在负权环，我们知道如果如果不存在负权环的话，经过 $V-1$ 次松弛操作后，dis 数组中的元素的值是不会再改变的，所以我们可以经过 $V-1$ 次松弛操作后再次进行一次松弛操作，如果在这次的松弛操作中，dis 中有元素的值发生改变，那么就说明存在负权环。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;

public class BellmanFord {
    private int[] dis;
    private WeightedGraph graph;
    private int s;
    private boolean hasNegativeCycle = false;
    private int[] pre;

    public BellmanFord(WeightedGraph graph, int s) {
        this.graph = graph;
        graph.validateVertex(s);
        this.s = s;
        this.dis = new int[graph.V()];
        this.pre = new int[graph.V()];

        Arrays.fill(dis, Integer.MAX_VALUE);
        Arrays.fill(pre, -1);
        dis[s] = 0;
        pre[s] = s;

        // k 代表轮数
        for (int k = 1; k < graph.V(); k++) {
            // 对所有边进行松弛操作，v-w 与 w-v 是两条边
            for (int v = 0; v < graph.V(); v++) {
                for (int w: graph.adj(v)) {
                    if (dis[v] != Integer.MAX_VALUE
                            && dis[v] + graph.getWeight(v, w) < dis[w]) {
                        dis[w] = dis[v] + graph.getWeight(v, w);
                        pre[w] = v;
                    }
                }
            }
        }

        // 再次进行一次松弛操作，检测负权环
        for (int v = 0; v < graph.V(); v++) {
            for (int w: graph.adj(v)) {
                if (dis[v] != Integer.MAX_VALUE
                        && (dis[v] + graph.getWeight(v, w) < dis[w])) {
                    hasNegativeCycle = true;
                }
            }
        }
    }

    public int[] result() {
        return dis;
    }

    public Iterable<Integer> path(int t) {
        ArrayList<Integer> path = new ArrayList<>();
        int cur = t;
        while (cur != s) {
            path.add(cur);
            cur = pre[cur];
        }
        path.add(s);

        Collections.reverse(path);
        return path;
    }
    
    public boolean isHasNegativeCycle() {
        return hasNegativeCycle;
    }
}

Floyed 算法

上面的两个算法解决的都是单源最短路径问题，而 Floyed 算法解决的所有点对之间的最短问题。我们其实可以通过使用 $V$ 次 Dijkstra 算法就可以求解所有点对之间的最短路径，不过 Dijkstra 算法不能处理负权边的问题，而 Floyed 算法可以处理负权边的问题。

但是同 Bellman-Ford 算法一样，如果图中存在负权环的话，就根本不存在最短路径，而我们知道如果无向图中有负权边的话，就相当于存在负权环，所以 Floyed 算法其实也是一个有向图算法。

Floyed 算法的思想也很简单，对于 v-w，假设它们之间的最短路径表示为 dis[v][w]，每一次都要尝试一下绕道点 t 会不会得到更短的路径(t 从节点 $0$ 取值到节点 $V-1$)，相当于

for(int t = 0; t < V; t++) {
    dis[v][w] = Math.min(dis[v][t] + dis[t][w], dis[v][w])
}

当经历过 $V$ 次的绕道尝试后，最终 dis[v][w] 就表示节点 v 与节点 w 之间的最短路径。

另外我们也可以通过 Floyed 算法对负权环进行检测，我们知道如果没有负权环的话 dis[v][v] 的值始终是 0，如果存在负权环的话，那么 dis[v][v] 的值就会更新为小于 0 的值，在经过 $V$ 次绕道之后检查所有的 dis[v][v] 是否等于 0 即可知道图中是否有负权环。

import java.util.Arrays;

public class Floyed {
    private WeightedGraph graph;
    private int[][] dis;
    private boolean hasNegativeCycle = false;

    public Floyed(WeightedGraph graph) {
        this.graph = graph;
        this.dis = new int[graph.V()][graph.V()];

        for (int i = 0; i < dis.length; i++) {
            Arrays.fill(dis[i], Integer.MAX_VALUE);
        }

        // 初始化 dis[][]
        for (int v = 0; v < graph.V(); v++) {
            dis[v][v] = 0;
            for (int w: graph.adj(v)) {
                dis[v][w] = graph.getWeight(v, w);
            }
        }

        // 绕道尝试
        for (int t = 0; t < graph.V(); t++) {
            for(int v = 0; v < graph.V(); v++) {
                for (int w = 0; w < graph.V(); w++) {
                    if (!(dis[v][t] == Integer.MAX_VALUE || dis[t][w] == Integer.MAX_VALUE)) {
                        dis[v][w] = Math.min(dis[v][w], dis[v][t] + dis[t][w]);
                    }

                }
            }
        }
        
        // 检测负权环
        for (int v = 0; v < graph.V(); v++) {
            if (dis[v][v] < 0) {
                hasNegativeCycle = true;
            }
        }
    }
    
    public int dis(int v, int w) {
        return dis[v][w];
    }
    
    public boolean isHasNegativeCycle() {
        return hasNegativeCycle;
    }
}

Floyed 算法也有时称为 3-for 算法，因为它的算法核心就是三个嵌套的 for 循环，Floyed 算法的实现是这三个算法中最简单的。

之前接触过的图都是无向图，在这个小节中讲解有向图

实际生活中的很多问题都可以建模为一个有向图的模型：

• 社交网络：图中的节点看做是一个个的人，如果一个节点指向一个节点，表示这个人关注了这个人，这种关注关系是有方向的
• 学习课程：将图中的节点看做是一门门的课程，一门课程被其他课程所指向，表示学习这门课程之前需要学习其他的课程，这种学习顺序也是有指向关系的
• 模块引用：将图中的节点看做是一个个的程序模块，一个模块被其他模块指向，表示该模块依赖于其他模块，这种模块之间的依赖也是有方向的

有向图算法

有向图的表示

我们之前介绍的无向图可以看做是一种特殊的有向图，所谓的特殊在于每个节点都互相指向。我们之前在 g.txt 值规定规定了节点之间的连接关系，所以我们当我们读取到下面的形式的时候

0 1

表示的是节点 0 指向节点 1 以及节点 1 指向节点 0，所以我们在无向图中实现如下

adj[0].add(1);
adj[1].add(0);

如果我们只是想表示节点 0 指向节点 1，我们就不需要添加下面那一行语句就好了。所以有向图对比于无向图的实现只需要更改这一个部分

{48}

import java.io.File;
import java.io.FileNotFoundException;
import java.util.Scanner;
import java.util.TreeSet;

public class DirectedGraph {
    private int E;
    private int V;
    private TreeSet<Integer>[] adj;

    public DirectedGraph(String filename) {
        File file = new File(filename);
        Scanner scanner = null;
        try {
            scanner = new Scanner(file);
            this.V = scanner.nextInt();
            if (this.V < 0) {
                throw new IllegalArgumentException("V Must Be Positive");
            }

            this.adj = new TreeSet[this.V];
            for (int i = 0; i < this.V; i++) {
                this.adj[i] = new TreeSet<>();
            }

            this.E = scanner.nextInt();
            if (this.E < 0) {
                throw new IllegalArgumentException("E Must Be Positive");
            }

            this.inDegree = new int[V];
            this.outDegree = new int[V];

            for (int i = 0; i < this.E; i++) {
                int a = scanner.nextInt();
                validateVertex(a);
                int b = scanner.nextInt();
                validateVertex(b);

                if (a == b) {
                    throw new IllegalArgumentException("Self loop exists");
                }
                if (adj[a].contains(b)) {
                    throw new IllegalArgumentException("Parallel edge exists");
                }

                // 只是删掉了 adj[b].add(a)
                adj[a].add(b);
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        } finally {
            assert scanner != null;
            scanner.close();
        }
    }

    private void validateVertex(int v) {
        if (v < 0 || v >= this.V) {
            throw new IllegalArgumentException("Vertex " + v + " is invalid");
        }
    }

    public int V() {
        return this.V;
    }

    public int E() {
        return this.E;
    }

    public Iterable<Integer> adj(int v) {
        validateVertex(v);
        return adj[v];
    }

    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder();
        stringBuilder.append(String.format("V: %d, E: %d\n", this.V, this.E));
        for (int v = 0; v < this.V; v++) {
            stringBuilder.append(String.format("%d : ", v));
            for (int w: adj(v)) {
                stringBuilder.append(String.format("%d ", w));
            }
            stringBuilder.append("\n");
        }
        return stringBuilder.toString();
    }
}

需要注意的是有一个概念同无向图有所不同，那就是度的概念，在有向图中度分为两类：

• 入度：有多少条边指向该节点
• 出度：有多少条件从该节点指向别的节点

例如对于下图，节点 2 的入度为 2，因为有两条边指向节点 2，出度为 1，因为有一条边从它指向节点 4。

所以我们再次修改一下类 DirectedGraph 如下

import java.io.File;
import java.io.FileNotFoundException;
import java.util.Scanner;
import java.util.TreeSet;

public class DirectedGraph {
    private int E;
    private int V;
    private TreeSet<Integer>[] adj;

    // 增加入度和出度的成员变量
    private int[] inDegree;
    private int[] outDegree;

    public DirectedGraph(String filename) {
        File file = new File(filename);
        Scanner scanner = null;
        try {
            // 其他代码相同

            this.inDegree = new int[V];
            this.outDegree = new int[V];

            for (int i = 0; i < this.E; i++) {
                // 其他代码相同

                adj[a].add(b);
                // 在这里初始化入度和出度，a → b，a的出度增加，b的入度增加
                inDegree[b]++;
                outDegree[a]++;
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        } finally {
            assert scanner != null;
            scanner.close();
        }
    }

    public int inDegree(int v) {
        validateVertex(v);
        return inDegree[v];
    }

    public int outDegree(int v) {
        validateVertex(v);
        return outDegree[v];
    }

    // 其他方法
}

DFS

对于有向图来说，它的 DFS 代码和 BFS 代码同无向图的写法完全是一样的，因为在后文中需要用到 DFS 遍历，所以这里贴出有向图的 DFS 遍历代码

import java.util.ArrayList;

public class DFSDirectedGraph {
    private DirectedGraph graph;
    // 深度优先前序遍历结果
    private ArrayList<Integer> pre;
    // 深度优先后序遍历结果
    private ArrayList<Integer> post;
    private boolean[] visited;

    public DFSDirectedGraph(DirectedGraph graph) {
        this.graph = graph;
        this.pre = new ArrayList<>();
        this.post = new ArrayList<>();
        this.visited = new boolean[graph.V()];

        for (int v = 0; v < graph.V(); v++) {
            if (!visited[v]) {
                dfs(v);
            }
        }
    }

    private void dfs(int v) {
        visited[v] = true;
        pre.add(v);
        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                dfs(w);
            }
        }
        post.add(v);
    }

    public ArrayList<Integer> pre() {
        return pre;
    }

    public ArrayList<Integer> post() {
        return post;
    }
}

可见上面的代码与无向图的 DFS 并无不同。

有向图的环检测

检测有向图中是否存在环是一件很有必要的事情

如果将上面的图看做是一个课程之间的依赖关系，如果图中存在环，说明课程之间相互依赖，学习课程 A 之前需要先学习课程 B，而学习课程 B 之前又需要先学习课程 A，这样的学习顺序肯定是有问题的。

我们想一想我们在无向图中是怎么做环检测的，我们使用 DFS 遍历，当遍历到一个节点时，如果某个邻接节点已经被访问了，并且不是它的父亲节点，我们就可以认为图中存在一个环。但是对于有向图就不一样了

上面的动图是优先遍历的顺序，最后我们来到了节点 3

此时我们发现节点 3 的相邻节点 2 已经被访问过了，并且节点 2 不是 3 的上一个节点，但是我们能说图中存在一个环吗? 不能，因为节点 2 无法到达节点 3，所以形成不了一个环。

此时我们需要另外一个变量来表示节点是否在路径上，如果一个节点访问邻接节点时发现该节点已经被访问过且在路径上，我们就可以说构成了一个环。

什么叫在路径上，如果这个节点还没有回溯到上一个节点，我们就说这个节点在路径上。

如果我们在访问到节点 w 时，节点 v 还在路径上，说明节点 v 可以到达节点 w，如果此时节点 w 可以到达节点 v 不就说明存在一个环吗。

public class DirectedCycleDetect {
    private DirectedGraph graph;
    private boolean[] visited;
    // onPath[w] 表示节点 w 是否在路径上
    private boolean[] onPath;
    private boolean hasCycle;

    public DirectedCycleDetect(DirectedGraph graph) {
        this.graph = graph;
        this.visited = new boolean[graph.V()];
        this.onPath = new boolean[graph.V()];
        this.hasCycle = false;

        for (int v = 0; v < graph.V(); v++) {
            if (!visited[v]) {
                if (dfs(v)) {
                    hasCycle = true;
                    break;
                }
            }
        }
    }

    private boolean dfs(int v) {
        visited[v] = true;
        onPath[v] = true;
        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                if (dfs(w)) {
                    return true;
                }
            // 通无向图不同，2 -> 1 -> 2 也是一个环
            } else if (onPath[w]) {
                return true;
            }
        }
        // 回溯到上一个节点时就不在路径上了
        onPath[v] = false;
        return false;
    }

    public boolean isHasCycle() {
        return hasCycle;
    }
}

拓扑排序

还是对于下面的这么一副图

假设上面的节点代表一门课程的话，我们想知道应该以什么样的顺序学习所有的课程，这其实就是在寻找图的拓扑排序。

那么我们寻找图的拓扑排序呢? 还是以学习课程举例，要学习一门课，那么这门就不能依赖于任何一门其他的课，或者这门课已经被学过了，就比如上面我们应该先学习课程 0，因为没有任何课程指向它，它不依赖于任何课程，以图论的语言来说，因为节点 0 的入度为 0，所以先学习课程 0。

学习完课程 0 之后，为了表示这门课程已经学过，我们将依赖于节点 0 的节点的入度减一

接下来我们应该学习哪门课呢? 当然是入度为 0 的课，表示不需要前置课程或者前置课程已经学过了，所以我们接下来学习课程 1，并且将依赖课程 1 的其他课程的入度减一

接下来还是学习入度为 0 的课程，即课程 3，并且更新依赖课程 3 的其他课程的入度

接着学习课程 2，因为它的入度为 0，然后更新依赖课程 2 的其他课程的入度

最后学习课程 4

所以最终课程的学习顺序为 0 → 1 → 3 → 2 → 4，也就是拓扑排序的结果。

所以我们对图做拓扑排序，就重复做两步：

• 选择入度为 0 的节点
• 更新相邻节点的入度

另外一个需要注意的问题就是，拓扑排序只对有向无环图(DAG) 有效，如果图中有环，二者相互依赖，就不知道先学习哪一门课程了。

在代码的实现方面，我们使用队列来存储入度为 0 的节点，在更新相邻节点入度的时候，如果入度为 0 则添加进队列中，每次从队列取出一个值时，我们添加到一个 List 中，表示拓扑排序的顺序。另外如果图中存在环的话，那么这个 List 中保存的节点数目肯定小于整个图的节点数目，此时可以使用拓扑排序来做环检测。

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;

public class TopoSort {
    private DirectedGraph graph;
    private int[] inDegree;
    private ArrayList<Integer> result = new ArrayList<>();
    private boolean hasCycle = false;

    public TopoSort(DirectedGraph graph) {
        this.graph = graph;
        this.inDegree = new int[graph.V()];

        Queue<Integer> queue = new LinkedList<>();
        for (int v = 0; v < graph.V(); v++) {
            inDegree[v] = graph.inDegree(v);
            if (inDegree[v] == 0) {
                queue.add(v);
            }
        }

        while (!queue.isEmpty()) {
            int v = queue.remove();
            result.add(v);
            for (int w: graph.adj(v)) {
                inDegree[w]--;
                if (inDegree[w] == 0) {
                    queue.add(w);
                }
            }
        }

        if (result.size() != graph.V()) {
            hasCycle = true;
            result.clear();
        }
    }

    public boolean isHasCycle() {
        return hasCycle;
    }

    public ArrayList<Integer> result() {
        return result;
    }
}

此时我们在介绍一种拓扑排序的算法，它需要借助于深度优先后序遍历。回顾一个后序遍历的概念，后序遍历指的是先访问完相邻节点，然后访问自己。

对于有向图意味着什么，意味着先访问依赖自己的节点，然后访问自己，说明自己是在依赖于自己的节点之后访问的，如果我们对深度优先后序遍历做一个逆序，这个顺序就表示自己在依赖于自己的节点之前被访问的，这不就是拓扑排序的结果吗。

使用深度优先后序遍历有一个缺点就是它不能做环检测，虽然图中有环，但是还是能够深度优先后序遍历，只不过此时结果便没有意义了。所以在使用这个方法做拓扑排序之前，我们需要使用我们之前讲解的有向图的环检测算法进行环检测

import java.util.ArrayList;
import java.util.Collections;

public class TopoSort2 {
    private DirectedGraph graph;
    private boolean hasCycle;
    private ArrayList<Integer> result = new ArrayList<>();

    public TopoSort2(DirectedGraph graph) {
        this.graph = graph;
        // 使用之前的讲解的环检测类进行环检测
        DirectedCycleDetect directedCycleDetect = new DirectedCycleDetect(graph);
        this.hasCycle = directedCycleDetect.isHasCycle();

        if (hasCycle) {
            return;
        }

        // 对图做深度优先后序遍历
        DFSDirectedGraph dfsDirectedGraph = new DFSDirectedGraph(graph);
        for (int v: dfsDirectedGraph.post()) {
            result.add(v);
        }
        // 对后序遍历取逆序
        Collections.reverse(result);
    }

    public boolean isHasCycle() {
        return hasCycle;
    }

    public ArrayList<Integer> result() {
        return result;
    }
}

强连通分量

现在还有一个问题就是我们怎么检测图中有多少个强联通分量，以及每一个强联通分量中包含哪些节点。所谓的强联通分量指如果某些节点互相可达，那么这些节点就组成了一个强联通分量。

如上图就三个强联通分量，每个联通分量内部的节点都是互相可达的。

在求解有向图的联通分量之前，我们回顾一下无向图的联通分量是如何求解的，我们从任意一个节点开始做 DFS，每次做一次 DFS 就表示有一个联通分量

for (int i = 0; i < visited.length; i++) {
    if (!visited[i]) {
        cccount++; // 联通分量个数增加
        dfs(i);
    }
}

但是对于有向图我们能从任意一个节点开始吗? 答案是不行，而是要以特定的顺序遍历。如果我们将一个个的联通分量看做是一个图中的节点

如果我们分别遍历联通分量 $E \rightarrow C \rightarrow A \rightarrow D \rightarrow B$ 中的节点，那么每做一次 DFS 就就可以统计联通分量数目，那么为什么会是上面的顺序呢?

为什么从 $E$ 开始遍历，因为 $E$ 只依赖其他联通分量的节点，没有其他联通分量依赖于它，所以从 $E$ 中的某个节点做 DFS，只能遍历到联通分量 $E$ 中的节点。同理遍历完了 $E$，此时 $C$ 也只依赖于其他联通分量，虽然 $E$ 依赖于 $C$，但是 $E$ 已经遍历完毕了，所以此时从 $C$ 中的节点开始做 DFS 只能遍历到 $C$ 中所有的节点，剩余的也是同理。

也就是说依赖于自己的联通分量要被先遍历到，也就是相邻节点要在自己之前被访问到，其实就是深度优先后序遍历的顺序，所以 $E \rightarrow C \rightarrow A \rightarrow D \rightarrow B$ 这个顺序其实是深度优先后序遍历的顺序。

但是这个深度优先后序遍历指的是以联通分量作为节点进行的遍历，如果我们从任意一个节点做深度优先后序遍历是得不到这个顺序的。例如我们从联通分量中的节点 $D$ 开始遍历，接着来到了联通分量 $C$，虽然遍历完联通分量 $C$ 中所有节点之前肯定需要遍历完联通分量 $E$，但是不能保证所有 $E$ 中的节点都在 $C$ 之前被遍历，即可能有这样的顺序 $C_1 \rightarrow E \rightarrow C_2 \rightarrow \cdots$，这样的顺序是我们不想要的，因为我们必须从联通分量 $E$ 中的节点开始遍历。

虽然上面的深度优先遍历不能严格按照 $E \rightarrow C \rightarrow A \rightarrow D \rightarrow B$ 的顺序遍历，但是我们发现一定有分量 $C$ 中的节点在分量 $E$ 遍历完之后遍历的 $C_1 \rightarrow E \rightarrow C_2 \rightarrow \cdots$，例如 $C_2$ 在遍历完 $E$ 之后被遍历了，这给了我们灵感，如果我们取个逆，就可以得到一定有 $C$ 中的节点在 $E$ 分量节点被遍历之前遍历。

而我们想要的是一定要 $E$ 中的节点在 $C$ 中的节点被遍历之前遍历，怎么办，我们将整个图的方向改变一下，原来是 $a \rightarrow b$，现在变为 $b \rightarrow a$

然后进行深度优先后序遍历，然后取个逆就可以保证一定有在 $E$ 中的节点在 $C$ 中的节点遍历之前被遍历到，同理可以得到一定有 $C$ 中的节点在 $D$ 中的节点被遍历之前被遍历到，这就达到我们的目的，我们再根据这个顺序做 DFS 就可以统计出联通分量的个数了。

上面这个算法就是 Kosaraju 算法，总结上面的步骤如下：

• 图翻转得到反图
• 对反图做深度优先后序遍历，然后对遍历结果取逆
• 根据取逆后的结果依次做 DFS，统计联通分量个数

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.TreeSet;

public class StrongCC {
    private DirectedGraph graph;
    private int[] visited;
    private int scccount;

    public StrongCC(DirectedGraph graph) {
        this.graph = graph;
        this.visited = new int[graph.V()];
        Arrays.fill(visited, -1);
        this.scccount = 0;

        // 翻转图
        TreeSet<Integer>[] reverse = new TreeSet[graph.V()];
        for (int i = 0; i < graph.V(); i++) {
            reverse[i] = new TreeSet<>();
        }
        for (int v = 0; v < graph.V(); v++) {
            for (int w: graph.adj(v)) {
                reverse[w].add(v);
            }
        }
        // 对翻转图做 DFS
        DFSDirectedGraph dfsDirectedGraph = new DFSDirectedGraph(new DirectedGraph(reverse));

        // 对深度优先后序遍历取逆
        ArrayList<Integer> res = dfsDirectedGraph.post();
        Collections.reverse(res);

        // 依次做 DFS，每做一次 DFS，联通分量个数增加
        for(int v: res) {
            if (visited[v] == -1) {
                dfs(v, scccount);
                scccount++;
            }
        }
    }

    private void dfs(int v, int id) {
        visited[v] = id;
        for (int w: graph.adj(v)) {
            if (visited[w] == -1) {
                dfs(w, id);
            }
        }
    }

    public ArrayList<Integer>[] components() {
        ArrayList<Integer>[] results = new ArrayList[scccount];

        for (int i = 0; i< scccount; i++) {
            results[i] = new ArrayList<>();
        }

        for (int v = 0; v < graph.V(); v++) {
            results[visited[v]].add(v);
        }
        return results;
    }
}

网络流

网络流与最大流

考虑一幅有向带权图

如果图中有一个源点，即入度为 0 的节点，上图的节点 0，有一个汇点，它的出度为 0，上图的节点 3，并且图中所有边的权值都是非负的，那么我们可以说这是一个网络流。

同一般的带权图不同，网络流中边的权值不是指从一个节点到达一个节点的距离是多少，耗费是多少，它指的是从一个节点到达另一个节点能够容忍的最大流量，例如从节点 0 到节点 1 它最多能够容忍 3 的流量。除了流量限制以外，还需要满足平衡限制，即流入某个节点的流量必须等于流出该节点的流量，即节点不允许存储流量，也不能产生流量(除了源点和汇点)。

真实世界中很多的问题可以建模为网络流的模型，例如供水系统，图中的边可以看做是水管，其中的权值表示的是水管能够通过的最大流量；又比如通信系统，每条边看做是一个信道，而权值可以看做是信道容量。

源点不断的发出流量，汇点不断接收流量，因为剩余的节点既不生产流量，也不存储流量，所以从源点发出的流量会全部进入到汇点。现在我们比较关心的是，从源点最多能发出多少流量，最终到达汇点，这就是最大流问题。

有向带权图

在讲解如何获得网络的最大流之前，我们先看看怎么表示网络流模型。其实网络流就是一个有向的带权图，我们只需要根据之前的无向带权图进行改造就可以得到有向带权图，改造的过程可以参考之前的无向无权图到有向无权图的改造，其实就是将

adj[v].put(w, weight);
adj[w].put(v, weight);

修改为了

adj[v].put(w, weight);

以此表明是一个有方向的图。另外为了实现后续的算法，我们为带权图增加了 2 个 API

• setWeight(v, w, weight)
• addEdge(v, w, weight)

另外我们还添加了一个新的构造方法，该方法只接收一个参数，即图中有多少个节点，得到一个没有边的图，在后续通过 addEdge 方法来图添加边。

DirectedWeightedGraph 类如下

import java.io.File;
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;

public class DirectedWeightedGraph{
    private int V;
    private int E;
    private HashMap<Integer, Integer>[] adj;

    public DirectedWeightedGraph(String path) {
        File file = new File(path);
        Scanner scanner = null;

        try {
            scanner = new Scanner(file);
            this.V = scanner.nextInt();
            if (V < 0) {
                throw new IllegalArgumentException("V can't be negative");
            }
            adj = new HashMap[V];
            for (int i = 0; i < V; i++) {
                adj[i] = new HashMap<>();
            }

            this.E = scanner.nextInt();
            if (E < 0) {
                throw new IllegalArgumentException("E can't be negative");
            }

            for (int i = 0; i < E; i++) {
                int v = scanner.nextInt();
                int w = scanner.nextInt();
                int weight = scanner.nextInt();

                if (v == w) {
                    throw new IllegalArgumentException("存在自环边");
                }
                if (adj[v].containsKey(w)) {
                    throw new IllegalArgumentException("存在平行边");
                }
			
                // 表示有向
                adj[v].put(w, weight);
            }
        } catch (Exception e) {
            e.printStackTrace();
        }finally {
            scanner.close();
        }
    }

    // 另一构造方法
    public DirectedWeightedGraph(int V) {
        this.V = V;
        this.E = 0;
        this.adj = new HashMap[V];
        for (int v = 0; v < V; v++) {
            adj[v] = new HashMap<>();
        }
    }

    public int V() {
        return this.V;
    }

    public int E() {
        return this.E;
    }

    public int getWeight(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        if (!hasEdge(v, w)) {
            throw new IllegalArgumentException(String.format("%d-%d 不存在", v, w));
        }
        return adj[v].get(w);
    }

    public void setWeight(int v, int w, int weight) {
        validateVertex(v);
        validateVertex(w);
        if (!hasEdge(v, w)) {
            throw new IllegalArgumentException(String.format("%d-%d 不存在", v, w));
        }
        adj[v].put(w, weight);
    }

    public void addEdge(int v, int w, int weight) {
        validateVertex(v);
        validateVertex(w);
        if (v == w) {
            throw new IllegalArgumentException("存在自环边");
        }
        if (adj[v].containsKey(w)) {
            throw new IllegalArgumentException("存在平行边");
        }

        adj[v].put(w, weight);
        E++;
    }

    public boolean hasEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return adj[v].containsKey(w);
    }

    public Iterable<Integer> adj(int v) {
        validateVertex(v);
        return adj[v].keySet();
    }

    public void validateVertex(int v) {
        if (v < 0 && v >= V) {
            throw new IllegalArgumentException("节点超过 [0, V) 的范围");
        }
    }

    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder();
        stringBuilder.append(String.format("V: %d, E: %d\n", this.V, this.E));
        for (int v = 0; v < this.V; v++) {
            stringBuilder.append(String.format("%d : ", v));
            for (Map.Entry w: adj[v].entrySet()) {
                stringBuilder.append(String.format("(%d: %d) ", w.getKey(), w.getValue()));
            }
            stringBuilder.append("\n");
        }
        return stringBuilder.toString();
    }
}

该类的大部分实现细节与无向的版本相似，如果不熟悉可以查看无向图的相关章节。

Ford-Fulkerson 思想

现在我们开始看一看如何找到图中的最大流，还是以下图为例

我们先从源点随便选择一条路径到达汇点

如上图我们就选择 $0 → 1 → 3$ 这条路径，这条路径能够允许的最大容量为 2，所以这条路径的流量为 2，为了表示已经通过了多少流量，我们以下面形式表示图

左边的数字表示已经通过了多少流量，右边的数字表示允许通过最大容量。接下来我们在选择一条路径

上面我们选择了 $0 → 1 → 2 → 3$ 这条路径，因为 $0 → 1$ 只允许 1 个流量通过了，所以这条路径的流量为 1，我们更新一下图

然后在选择一条路径

这次我们选择了 $0 → 2 → 3$，这条路径的流量为 $2$，更新图如下

接下来我们我们找不到一条路径从源点到汇点了，所以此时我们可以说该网络流的最大流为 $2 + 1 + 2 = 5$。

所以上面的算法就是重复下面两步：

• 随便找一条路径从源点到汇点，找到路径的最小值，就是这条路径的流量
• 更新每条边允许通过的流量

但是真的随便找一条路径就可以吗? 显然不行，例如我们一开始就找到了这么一个路径

这条路径的流量为 3，我们更新图

但是接下来我们发现找不到路径从源点到汇点了，所以我们得出这个网络流的最大路径为 $3$，明显这个答案是不对的，所以我们不能随便选择路径走，因为可能得不到正确的答案。

但是，如果我们允许反向流动呢? 例如还是以上图为例

这次我们选择路径如下

更新后的图为

本来从 $2 → 1$ 是不可达的，但是我们赋予它一个语义，表示将原来通过 $1 → 2$ 的流量引导到别的路径去了，例如本来 $1 → 2$ 有流量为 3，现在我们反向流动 2 个流量，表示将原来这 3 个流量中的 2 个流量引导到别的路径中去了。

赋予这么一个语义的话，那么上面图的所有箭头都可以变为双向的，反向的箭头表示允许被引导到别的路径上，我们给它一个权值，表示能够被允许引导到别的路径上去的流量的最大值，这个值应该是已经通过该路径的流量，例如如果 $1 → 2$ 是用 $3/5$ 表示的话，表示已经有 $3$ 个流量通过 $1 → 2$，那么$2 → 1$ 最多允许 $3$ 个流量被引导。

为了表示方便，不用 $3/5$ 这样的形式来标记边了，而是以剩余允许通过的流量表示边，例如 $3/5$ 表示最大容量为 $5$，已经通过流量为 $3$，所以剩余能够通过的流量为 $2$，我们以 $2$ 来标记这条边，同理我们也以这样的方式标记反向的边，得到下面的这么一个图

黑色表示正向边，红色表示反向边，上面的数值表示能够允许通过的最大流量，可见在最开始反向边是不能允许通过流量的，它们的权值都是 0，这个图我们称之为残差图。

接下下我们就可以使用上面提到的两步了：

• 随便找一条路径从源点到汇点，找到路径的最小值，就是这条路径的流量
• 更新每条边允许通过的流量

这个方法就是 Ford-Fulkerson 思想。

Edmonds-Karp 算法

上面的 Ford-Fulkerson 只是提供了一种思想，得到一个网络流的残差图，然后随便找一条路径从源点到汇点，但是没有说怎么找这条路径，所以它只是一种思想。

接下来我们就介绍 Edmonds-Karp 算法，它就是为 Ford-Fulkerson 提供了一种具体的实现，怎么找一条路径，很简单，那就是从源点进行 BFS 来找到一条路径，当我们通过 BFS 无法达到汇点时，说明网络不能够承受更大的流量了。

所以上面的方法是不是非常的简单，下面就给出具体的实现

import java.util.*;

public class MaxFlow {
    private DirectedWeightedGraph graph;
    private int s;
    private int t;
    private DirectedWeightedGraph rcGraph;
    private int maxFlow = 0;

    public MaxFlow(DirectedWeightedGraph graph, int s, int t) {
        this.graph = graph;

        // 一些校验工作
        if (graph.V() < 2) {
            throw new IllegalArgumentException("网络流中节点个数必须大于1");
        }
        graph.validateVertex(s);
        graph.validateVertex(t);
        this.s = s;
        this.t = t;

        // 根据传入的网络流，构造残差图
        DirectedWeightedGraph rcGraph = new DirectedWeightedGraph(graph.V());
        for (int v = 0; v < graph.V(); v++) {
            for (int w: graph.adj(v)) {
                rcGraph.addEdge(v, w, graph.getWeight(v, w));
                // 一开始反向边能够允许通过的最大流量为 0
                rcGraph.addEdge(w, v, 0);
            }
        }
        this.rcGraph = rcGraph;

        while (true) {
            // 开始从源点做 BFS
            ArrayList<Integer> path =  getAugmentPath();
            // 如果从 BFS 得到的路径为空，说明不能到达汇点了，此时退出循环
            if (path.size() == 0) {
                break;
            }

            // 获得路径的最小值，即这条路径允许通过的最大流量
            int min = Integer.MAX_VALUE;
            for (int i = 1; i < path.size(); i++) {
                int v = path.get(i - 1);
                int w = path.get(i);

                min = Math.min(min, rcGraph.getWeight(v, w));
            }

            maxFlow += min;

            // 更新残差图
            for (int i = 1; i < path.size(); i++) {
                int v = path.get(i - 1);
                int w = path.get(i);

                rcGraph.setWeight(v, w, rcGraph.getWeight(v, w) - min);
                rcGraph.setWeight(w, v, rcGraph.getWeight(w, v) + min);
            }
        }
    }

    // 做 BFS
    private ArrayList<Integer> getAugmentPath() {
        Queue<Integer> queue = new LinkedList<>();
        int[] pre = new int[graph.V()];
        queue.add(s);
        Arrays.fill(pre, -1);
        pre[s] = s;

        while (!queue.isEmpty()) {
            int v = queue.remove();
            for (int w: rcGraph.adj(v)) {
                if (pre[w] == -1 && rcGraph.getWeight(v, w) > 0) {
                    pre[w] = v;
                    queue.add(w);
                }
            }
        }

        ArrayList<Integer> result = new ArrayList<>();
        if (pre[t] == -1) {
            return result;
        }

        int cur = t;
        while (cur != s) {
            result.add(cur);
            cur = pre[cur];
        }
        result.add(s);
        Collections.reverse(result);
        return result;
    }

    // 返回网络的最大流
    public int result() {
        return maxFlow;
    }

    // 返回最终 v-w 允许通过的流量
    public int flow(int v, int w) {
        if (!graph.hasEdge(v, w)) {
            throw new IllegalArgumentException("存在这条边");
        }
        graph.validateVertex(v);
        graph.validateVertex(w);

        return rcGraph.getWeight(w, v);
    }
}

棒球比赛

最后我们看一个使用最大流解决实际问题的例子，那就是棒球比赛。

全美每年都会举行一次棒球比赛，每个队都要进行 162 场比赛，最终所胜的场次最多的队伍获胜，如果平局就进行加赛。

但是如果在比赛的过程中，某一队已经没有获得冠军的希望了，那么该队就会被直接淘汰。例如 $A$ 队已经赢了 $10$ 场了，而 $B$ 队只赢了 $1$ 场，并且还有 $8$ 场比赛没有打，此时 $B$ 队如何也不能赢的场次比 $A$ 队多，所以 $B$ 队应该被淘汰。

现在我们拿到了 1996 年 8 月 30 日真实的比赛数据，此时只剩下 5 个队

Teams	Wins	Loss	Left	Against	NY	Bal	Bos	Tor	Det
New York	75	59	28		0	3	8	7	3
Baltimore	71	63	28		3	0	2	7	4
Boston	69	66	27		8	2	0	0	0
Toronto	63	72	27		7	7	0	0	0
Detroit	49	86	27		3	4	0	0	0

Wins 代表赢了多少场，Loss 表示输了多少场，Left 表示剩余多少场没有打，Against 后面的 5 列表示与其他队要打多少场。

当时媒体争议的是最后一个队，即 Detroit 队还有没有获胜的希望。从数据上看，如果 Detroit 剩下的 27 场全赢，那么它的赢的总场次是 $49 + 27 = 76$，比最强的 New York 还多一场，所以它还有赢的机会，但是这样想的话就忽略了一个事实，即使 Detroit 与其他四队的比赛都打赢了，但是这四个队之间还有比赛，也就说说这四个队它们的总胜场是会增加的。

所以现在又变为了这么一个问题，如果前四个队之间比赛，如果最终它们的胜场最多是 76 的话，说明 Detroit 队还有赢的希望，否则 Detroit 队没有赢的可能。现在我们如下建模

这个图分为三部分，第一部分

其中权值表示比赛场次，比如 s → NY-Bal 这条边的权值为 $5$，表示 NY 与 Bal 之间有五场比赛要打，可见这四个队伍总共要打 $5 + 8 + 7 + 2 + 7 = 27$ 场比赛。第二部分

这次的权值表示的是胜场的分配。第三部分

这时其中的权值表示每个队最多赢多少次，例如 NY 队目前 $75$ 分，它最多只能赢一场。如果上述网络流的最大流大于等于比赛的总场次，所以存在一种方案能够分配所有胜场使得所有队的得分最多只有 $76$ 分。

上面网络流我们建模为如下图

11 19
0 1 3
0 2 8
0 3 7
0 4 2
0 5 7
1 6 3
1 7 3
2 6 8
2 8 8
3 6 7
3 9 7
4 7 2
4 8 2
5 7 7
7 9 7
6 10 1
7 10 5
8 10 7
9 10 13

现在我们用之前写的 MaxFlow 类来查看最大流是多少

public class BaseBallSolution {
    public static void main(String[] args) {
        DirectedWeightedGraph baseball = new DirectedWeightedGraph("g17.txt");
        MaxFlow maxflow = new MaxFlow(baseball, 0, 10);
        System.out.println(maxflow.result());
    }
}

结果是

26

说明最大流为 26，小于 27，说明无法分配 27 场比赛使得所有队最多只能赢 76 场，这就意味着 Detroit 没有赢的可能了。

匹配问题

最大匹配与完全匹配

下面我们讲解的算法都是有关于二分图的算法

例如对于上图就是一个二分图，每条边都连接了两个不同部分的节点，生活中很多问题都可以建模为二分图的问题，例如相亲。左边表示男生群体，右边表示女生群体，如果两个节点之间有一条边，说明这一对男女可以匹配为一对；另外又比如求职，左边的节点表示求职者，右边的节点表示公司，如果节点之间有一条边，表明求职者与公司互相都比较满意，可以匹配。

现在我们关心的问题是，向这样的二分图最多有多少个匹配，这样的问题称为最大匹配问题，如果最大匹配的个数与左右两边的节点数目都相同，那么就称为是完全匹配，对于相亲来说，意味着每一个人都可以找到另一半，对于求职来说，每个求职者都可以找到一家公司。

最大流解决匹配问题

解决最大匹配问题的一个方案就是将上面的图建模为一个网络流

图中的每一条边的权值都为 1，即每条边的允许通过的最大流量为 1，表示每一个节点都只能被匹配一次，此时这个网络流的最大流就等于最大匹配数，我们将求二分图的最大匹配问题转化为了求网络流的最大流问题，而求最大流的问题我们在以前已经接触过。

我们唯一需要的工作量就是根据上面的二分图得到一个网络流的模型，具体见代码

public class BipartiteMatching {
    private Graph graph;
    private int maxMatching;

    public BipartiteMatching(Graph graph) {
        this.graph = graph;
        // 首先对是否是二分图进行检测
        BinaryPartitionDetection bpd = new BinaryPartitionDetection(graph);
        if (!bpd.isBipartite()) {
            throw new IllegalArgumentException("该图不为一个二分图");
        }
        int[] colors = bpd.colors();

        // 根据二分图建模为网络流，多添加的两个节点为源点和汇点，源点编号为 V，汇点为 V + 1
        DirectedWeightedGraph directedWeightedGraph = new DirectedWeightedGraph(graph.V() + 2);
        for (int v = 0; v < graph.V(); v++) {
            // colors[v] == 0 表明是左边的节点，被源点指向
            if (colors[v] == 0) {
                directedWeightedGraph.addEdge(graph.V(), v, 1);
            } else {
                // colors[v] == 1 表示是右边的节点，执行汇点
                directedWeightedGraph.addEdge(v, graph.V() + 1, 1);
            }

            for (int w: graph.adj(v)) {
                if (v < w) {
                    // 左边的节点指向右边的节点
                    if (colors[v] == 0) {
                        directedWeightedGraph.addEdge(v, w, 1);
                    } else {
                        directedWeightedGraph.addEdge(w, v, 1);
                    }
                }
            }
        }

        // 建立网络流，获得最大流
        MaxFlow maxFlow = new MaxFlow(directedWeightedGraph, graph.V(), graph.V() +1);
        maxMatching = maxFlow.result();
    }

    public int result() {
        return maxMatching;
    }

    // 如果最大匹配的两倍等于图中的节点数，说明是完全匹配
    public boolean isPerfectMatching() {
        return maxMatching * 2 == graph.V();
    }
}

上面对二分图检测以及最大流的类在之前文章讲解过，不多加介绍。

LCP04 覆盖

LCP04 覆盖是一道 LeetCode 上的题目，我们可以将这道题建模为二分图的最大匹配问题。

题目介绍

你有一块棋盘，棋盘上有一些格子已经坏掉了。你还有无穷块大小为 $1 * 2$ 的多米诺骨牌，你想把这些骨牌不重叠地覆盖在完好的格子上，请找出你最多能在棋盘上放多少块骨牌? 这些骨牌可以横着或者竖着放。

• 输入：n, m代表棋盘的大小；broken是一个 $b * 2$ 的二维数组，其中每个元素代表棋盘上每一个坏掉的格子的位置。

• 输出：一个整数，代表最多能在棋盘上放的骨牌数。

解题思路

对于棋盘问题，如果玩过国际象棋的话，就知道棋盘是被染为黑白两色的，如

同理我们也可以将上面的棋盘根据上面的染色分为两个区域，如果将网格上的一个个网格看做是图中的节点的话，这不就是一个二分图吗? 而对一个 $1 * 2$ 的多米诺骨牌，它总是一边在黑色区域，一边在白色区域，题目问能够放置多少块多米诺骨牌不就是在问该二分图的最大匹配图吗?

因为我们成功的将上面的问题建模为了二分图的最大匹配，可以利用我们上面的算法进行解决，现在唯一的难点可能就是将上面的网格建模为一个图了，代码如下

import java.util.*;

public class Solution {
    public int domino(int n, int m, int[][] broken) {
        int[][] board = new int[n][m];

        // 1 表示格子坏掉了，0 表示格子是好的
        for (int[] p: broken) {
            board[p[0]][p[1]] = 1;
        }

        // 将网格建模为一个图
        AdjSet graph = new AdjSet(n * m);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                // 我们只添加右边和下面的节点，因为左边的节点的右边就是自己，不用重复添加，同理对于上面也是
                if (j + 1 < m && board[i][j] == 0 && board[i][j + 1] == 0) {
                    graph.addEdge(i * m + j, i * m + j + 1);
                }

                if (i + 1 < n && board[i][j] == 0 && board[i + 1][j] == 0) {
                    graph.addEdge(i * m + j, (i + 1) * m + j);
                }
            }
        }

        BipartiteMatching bm = new BipartiteMatching(graph);
        return bm.result();
    }
}

匈牙利算法

解决匹配问题的另一个算法就是匈牙利算法，还是以下图为例

匈牙利算法的思想就是每次从左边未匹配的点出发进行遍历，如果右边的点没有匹配，则将它们匹配为一对

上面我们从节点 0 出发，来到节点 4，发现节点 4 没有被匹配，因此将它们设置为匹配，我们使用一个数组来进行记录

matching[0] = 4;
matching[4] = 0;

如果右边的节点已经被遍历了，则从右边节点匹配的节点继续遍历，例如对于下图，我们从 1 出发，来到节点 4，发现节点 4 已经被遍历了，于是来与节点 4 匹配的节点 0，然后从 0 开始向右遍历，直到向右找到一个未匹配的节点

上面我们遍历的路径是 $1 → 4 → 0 → 6$，本来 0-4 是匹配的，现在我们让它断开，让 1-4、0-6 匹配。

重复上面的过程，每次如果在右边找到一个未匹配的节点，匹配数加一，当我们遍历完左边所有的未匹配的节点时，最终的匹配数就是最大匹配数，这就是匈牙利算法。

这里总结一下匈牙利算法的流程：

• 从左边未匹配的节点遍历，如果右边的节点未匹配，那么让二者匹配，匹配数加一
• 否则右边的节点已匹配，那么从右边节点匹配的节点继续遍历
• 重复上面的过程，直到找到一个右边未匹配的节点，那么匹配数加一，并且更新匹配关系

根据遍历的顺序不同，匈牙利算法有两种实现，一种是使用 BFS 进行遍历，该种方法速度较快，但是代码复杂

import java.util.*;

public class HungarianBFS {
    private Graph graph;
    private int[] matching;
    private int maxMatching;

    public HungarianBFS(Graph graph) {
        this.graph = graph;
        // 先检测是否是二分图
        BinaryPartitionDetection bpm = new BinaryPartitionDetection(graph);
        if (!bpm.isBipartite()) {
            throw new IllegalArgumentException("该图不是二分图");
        }
        this.matching = new int[graph.V()];
        Arrays.fill(matching, -1);

        int[] colors = bpm.colors();

        for (int v = 0; v < graph.V(); v++) {
            // colors[v] == 0 说明是左边节点
            // matching[v] == -1 说明未匹配，从这种节点开始遍历
            if (colors[v] == 0 && matching[v] == -1) {
                // bfs 的返回值表示是否找到一个右边未匹配的节点
                if (bfs(v)) {
                    // 找到匹配数就加一
                    maxMatching++;
                }
            }
        }
    }

    // 进行 bfs 遍历
    private boolean bfs(int v) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(v);
        int[] pre = new int[graph.V()];
        Arrays.fill(pre, -1);
        pre[v] = v;
        while (!queue.isEmpty()) {
            int cur = queue.remove();
            for (int next: graph.adj(cur)) {
                if (pre[next] == -1) {
                    // 如果右边的节点已经匹配了
                    if (matching[next] != -1) {
                        // 从右边节点的匹配节点开始继续遍历
                        queue.add(matching[next]);
                        pre[next] = cur;
                        pre[matching[next]] = next;
                    } else {
                        // 右边的节点未匹配，找到了，更新匹配关系
                        pre[next] = cur;
                        ArrayList<Integer> path = getPath(pre, v, next);
                        for (int i = 0; i < path.size(); i += 2) {
                            matching[path.get(i)] = path.get(i + 1);
                            matching[path.get(i + 1)] = path.get(i);
                        }

                        return true;
                    }
                }
            }
        }

        return false;
    }

    private ArrayList<Integer> getPath(int[] pre, int start, int end) {
        int cur = end;

        ArrayList<Integer> result = new ArrayList<>();

        while (cur != start) {
            result.add(cur);
            cur = pre[cur];
        }
        result.add(start);
        Collections.reverse(result);
        return result;
    }

    public int result() {
        return maxMatching;
    }
}

还有一种实现是使用 DFS 进行遍历，虽然比 BFS 慢一丢丢，但还是实现简单

import java.util.Arrays;

public class HungarianDFS {
    private Graph graph;
    private int maxMatching;
    private boolean[] visited;
    private int[] matching;

    public HungarianDFS(Graph graph) {
        // 下面的初始化逻辑同 BFS
        this.graph = graph;
        BinaryPartitionDetection bmp = new BinaryPartitionDetection(graph);
        if (!bmp.isBipartite()) {
            throw new IllegalArgumentException("该图不是二分图");
        }
        int[] colors = bmp.colors();
        this.maxMatching = 0;
        this.visited = new boolean[graph.V()];
        this.matching = new int[graph.V()];
        Arrays.fill(matching, -1);

        for (int v = 0; v < graph.V(); v++) {
            // 左边未匹配节点开始遍历
            if (colors[v] == 0 && matching[v] == -1) {
                Arrays.fill(visited, false);
                // dfs 返回值的含义同 bfs
                if (dfs(v)) {
                    maxMatching++;
                }
            }
        }
    }

    private boolean dfs(int v) {
        visited[v] = true;

        for (int w: graph.adj(v)) {
            if (!visited[w]) {
                visited[w] = true;
                // 如果右边未匹配，更新匹配关系
                // 或者右边已匹配，并且从右边已匹配的节点遍历能找到一个右边未匹配的节点，也更新匹配关系
                if (matching[w] == -1 || dfs(matching[w])) {
                    matching[v] = w;
                    matching[w] = v;
                    return true;
                }
            }
        }

        return false;
    }

    public int result() {
        return maxMatching;
    }
}

同理我们可以使用匈牙利算法来完成上面的 LeetCode 问题

import java.util.*;

public class Solution {
    public int domino(int n, int m, int[][] broken) {
        int[][] board = new int[n][m];

        for (int[] p: broken) {
            board[p[0]][p[1]] = 1;
        }

        AdjSet graph = new AdjSet(n * m);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (j + 1 < m && board[i][j] == 0 && board[i][j + 1] == 0) {
                    graph.addEdge(i * m + j, i * m + j + 1);
                }

                if (i + 1 < n && board[i][j] == 0 && board[i + 1][j] == 0) {
                    graph.addEdge(i * m + j, (i + 1) * m + j);
                }
            }
        }

        HungarianBFS hungarianBFS = new HungarianBFS(graph);
        return hungarianBFS.result();
    }
}

速度比使用网络流要快